常常聽說“物理學大廈”的比喻,比如大廈裏的這個房間是“熱力學”,那個房間是“牛頓力學”,那邊那個是“量子力……既然是大廈,那在裏面順便養點可可愛愛的小動物不過分吧?
多年以來,大廈住戶衆多,因此動物(在對物理學進行討論的過程中,人們提出的各樣載體和假設,算是一種思想實驗)也不少,其中相當知名的便是物理學四大神獸——芝諾的龜龜、拉普拉斯妖、麥克斯韋妖、薛定諤的可愛貓貓。

看看老芝
從時間順序來說,芝諾的烏龜是最早提出的,說是在公元前五世紀,古希臘人芝諾(芝諾的烏龜當然是芝諾提出來的啦,然而洛必達法則並不是洛必達提出的)在阿基里斯前1000米初放了一隻烏龜讓他去追,在相同時間t內,阿基里斯每跑10s(s>0)米,烏龜就會前進s米,也就是說,阿基里斯跑完1000米的時候烏龜在前方100米,阿基里斯跑完100米的時候烏龜在前方10米處……二者的距離會發生這樣的變化“1000—>100—>10—>1—>0.1—>……”,無限趨近於0。

跑得比烏龜還慢(惱)
極限問題
龜人賽跑的故事實在是廣爲人知,師出同門的河流無限細分悖論聽起來則會更加新奇、耐人尋味,現在假如張三要過河,他可以這樣看待這個問題:
可以將河流平均分爲兩等份,先走前面一半再走剩下一半(1/2),而前面一半和剩下一半也都可以被均分,先走前面一半的一半(1/4),而後以此類推(1—>1/2—>1/4—>1/8—>1/16……),這就有了無限分割出來的很小的一半,而每個一半都要相應的時間t,t乘上無窮個一半,不就是無窮嗎?
因此張三過河需要的時間是無窮久。

張三:困惑🤔
不是問題
河流問題在理解上比龜人賽跑要抽象,但在實踐上卻簡單得多,因爲我們僅憑日常生活的經驗就可以知道張三是錯的——這是最淺層、最簡單的解釋。
從運動的屬性來看,現實中的運動是連續而自然的,因此並不能用“完成一個時間和空間上無限小的步驟後再完成下一個,直到完成無限個”的模型進行套用,更簡單地說,現實中的運動不能進行這樣的拆分,我們在數學和物理上只是爲了方便計算和精簡模型纔會這麼做的。
從時空本身的性質看,時空本身是可以無限拆分的嗎?這似乎和某些量子力學領域的某些假設產生了衝突,倘若時空只能細分到普朗克尺度,那麼就根本不會存在“無限分割出來的很小的一半”,它實際上應當是有限的,只不過數量很多而已。
從數學角度來看,這實際上是一個微積分的問題,在已知條件充足的情況下,使用一定的數學技巧就可以算出過河流的時間,提供最直接又客觀的答案。
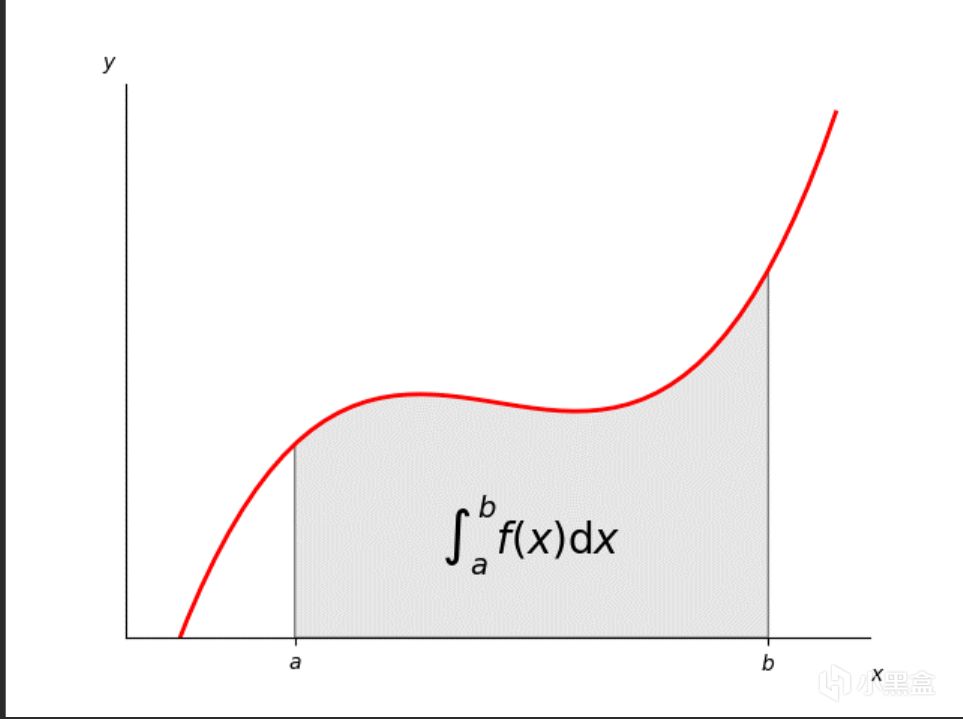
所以爲什麼過河要用微積分?應該是爲了幫助人知其然知其所以然吧,建立一個自洽的科學理論解釋問題,然後不斷修補、推翻、應用它,大概就是這樣的。
更多遊戲資訊請關註:電玩幫遊戲資訊專區
電玩幫圖文攻略 www.vgover.com


















