什么是逻辑解谜?这个词并没有一种大家都承认的定义,但我个人将其定义为“基于一套可以用严谨的数学语言表述的底层规则/逻辑的解谜”,不管这套规则实际上表述起来有多复杂。比如大家耳熟能详的《推箱子》就可以用“有限状态机”这样的东西给出一套严谨的定义,但我在这里就不定义给大家看了。而至于《锈湖》这样的指向点击解谜,虽然可能内含单个的逻辑谜题,但大多数不属于我所定义的“逻辑解谜”。
对于这类游戏,我不止一次听到这样的声音:“这种游戏就和做题一样,没什么意思”。这我并不完全否认,但肯定也不完全同意。“像做题”这个表述比较笼统,到底是在哪方面“像”呢?是说逻辑解谜和做题一样重复和枯燥无味吗?还是说逻辑解谜和做题一样,一旦不会就只能看答案,只是因为没有出题人一般的超强“注意力”?
我不知道屏幕前的你有没有看过“3Blue1Brown”这位知名数理科普博主的视频,我也不止一次看到有评论说这个频道“重新点燃了其对数学的热情”。举这个例子是想表明,我认为并不是“数学”或者“数学题”本身枯燥,有可能我们只是没有掌握正确的思维方法,对于逻辑解谜当然也是一样。
所以这篇文章的目的就此显现:我希望通过分享我个人游玩逻辑解谜的经验,包括我的解谜思路和“技巧”,来让大家感受到逻辑解谜游戏中蕴含的逻辑之美。

游戏:Jonathan Blow开发中的推箱子新作
(有些插图只是为了让文章看上去没那么“干”,当图片真的和文字有关的时候我会说的)
我不太清楚屏幕前的各位之前是怎么“解谜”的,我觉得无论你熟不熟悉解谜游戏,也不管你能不能将你自己的思路明确表达出来,只要你尝试过解谜,在你大脑中一定有某个部分负责这个过程当中的逻辑思维,尽管你可能觉得这只是某种“直觉”,或者是某种专属于所谓“大佬”的“注意力”。
而且,几乎所有的解谜游戏攻略只包含实际上“输入”解谜步骤的过程,而不包含解谜背后的思维方法,这就更会加深玩家对深度解谜玩家的“刻板印象”,认为“他们就是比我聪明”或者“他们就是注意力比我强”。
解谜游戏不是搞学术,因此不需要“防御性证明”(只能看出来是对的,但完全看不出来是怎么想出来的)。我在这里想做的,就是尝试把这些背后的“直觉”明确地表述出来,从而给大家展示我自己解谜时,遇到靠直觉无法解决的谜题时(也就是大部分时候),我能从什么角度去思考问题。
下面,我会先列举一些在我看来有用的解谜策略,然后用一些具体谜题的例子手把手带大家领略我自己的解谜思路。
策略一:试错
这可能是大部分玩家碰到无法立刻通过的谜题时的第一反应,毕竟如果胡乱试一试就能通过的话,为什么要动脑呢?虽然很简单粗暴,但又不得不承认,在某些情况下,试错确实就是最有效率的做法。
具体来说,这种策略就像是在走迷宫:
从起点出发,找到一条符合直觉的路往下走,如果走不通,就倒回去,在最后一个岔路选择另一条路走,一直走到终点为止。而在大多数的逻辑解谜游戏中,关卡状态的变化实际上就形成了“隐式”的迷宫,那么当然也就可以使用类似的策略。
然而,试错策略仍然具有下列问题:
绝大多数逻辑解谜的“状态迷宫”都不如上面图片中的迷宫这么容易理解,不太可能“纵览全局”。在逻辑解谜游戏中,试错的体验其实更接近“第一人称走迷宫”,手上没有地图的那种。
考虑到上面这一点,有时要记住自己探索过哪些方向也是非常困难的。我到底有没有走过这条路?有没有到过这个岔路口?有时,我们甚至很难看出一个局面下的所有可行选择,更别说枚举了。稍有不慎就可能有重复或遗漏,导致你在状态迷宫中“迷路”。
如果一个谜题看上去有太多的可能性,完全不能枚举,那么试错策略明显就不管用了。就算能用,很多时候通过试错来解谜也并不会产生核心的“尤里卡”时刻,因为这和模拟计算机搜索没什么区别,没有什么独属于人类的“逻辑美感”。
那这个时候怎么办呢?放弃吗?当然不是。我们首先想一想,“试错”的本质是什么?是通过亲自探索来确认每条“路”是能走通还是走不通。那如果我们有办法,不用亲自把每一条岔路都走完,就知道它们能不能走通呢?
恭喜你,你刚刚发现了“剪枝”的思想,而接下来要说到的所有策略,本质上都是通过人类逻辑做到了剪枝。
策略二:寻找瓶颈步骤
我觉得说这是我个人在解谜中用到的最重要的策略也不为过。它是很多种小策略的集合,但是目标一致,所以就直接合起来说了。
瓶颈步骤就是在解决一个谜题过程中必须要经过的步骤。继续以“迷宫”为例:
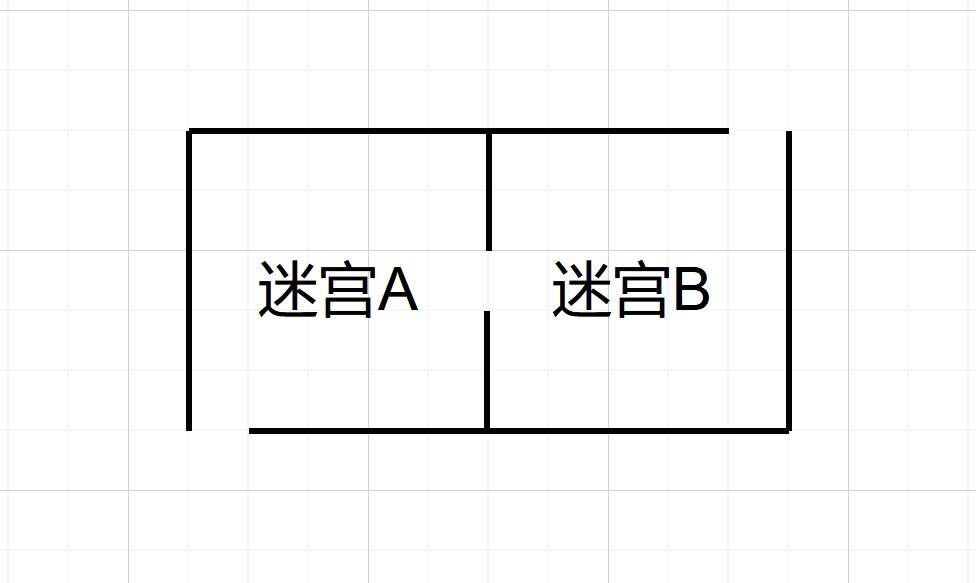
假设有这么一个迷宫,你需要从左下角到达右上角,而迷宫中间有一条明显的分界线,且分界线中间只有一个开口。在考虑正常解法(即不能从外面走,不能穿墙,等等)的前提下,你能够获得什么结论?没错,那就是路线必须要经过中间那个开口。
那这又有什么帮助呢?可以看出,整个迷宫现在就被分界线分成了“迷宫A”和“迷宫B”两个部分,现在你只需要分开解决两个迷宫就可以解开整个迷宫了。
是的,找到瓶颈步骤最大的作用,就是将谜题这个“大问题”分成更多更容易的“小问题”,这也就是经典的“分治”思想。
比如对于上面的第一个迷宫,我们就可以找到下面标红的“分界线”:
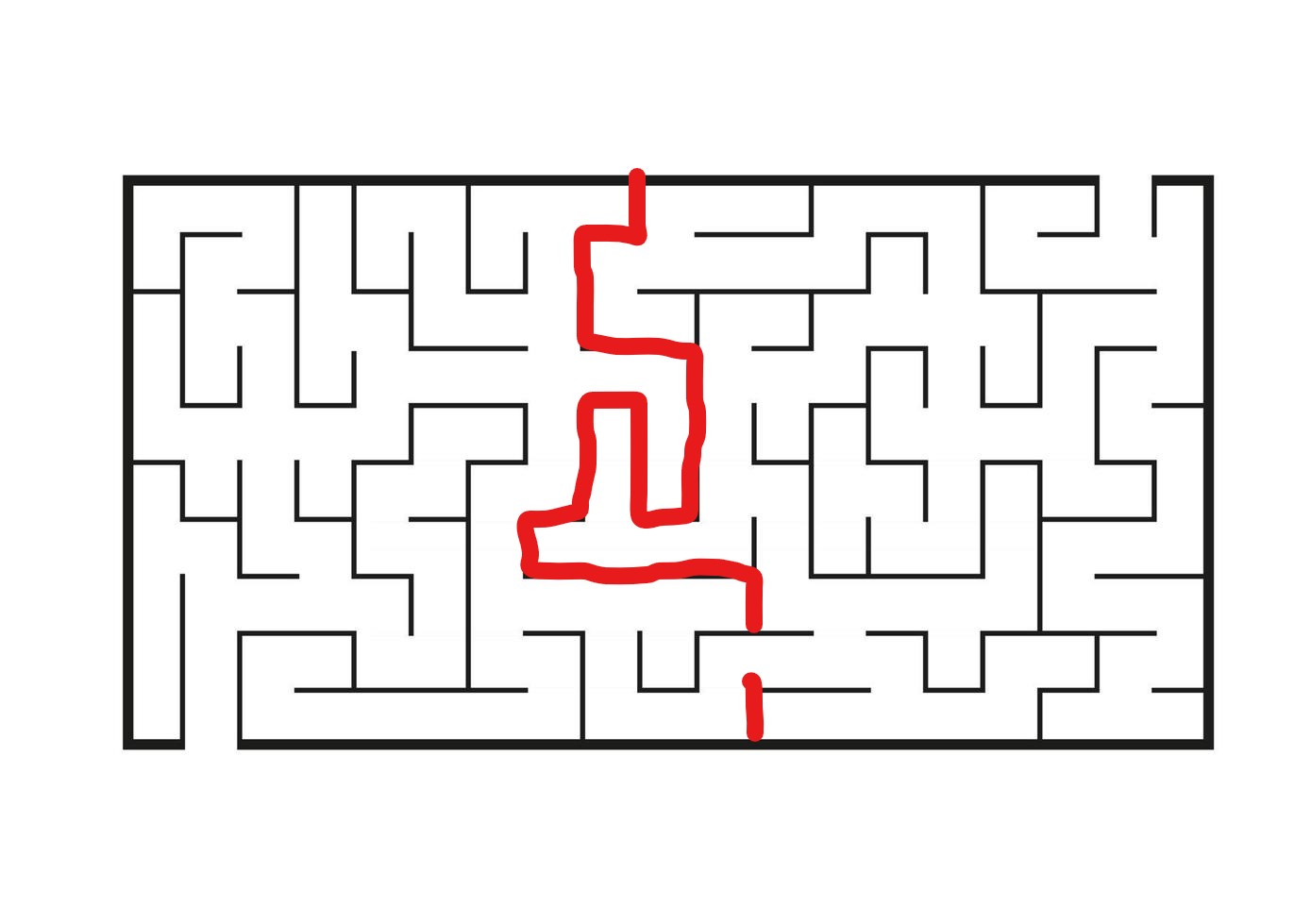
当然这只是举个简单的例子,如果你可以用其它更简单的方式解开谜题,那自然没有必要用到更复杂的策略。只不过,在实际应用中,很多时候你面对的问题都并不像这个迷宫这么简单,此时找到一些关键的瓶颈步骤就能大大减少试错的量。
要寻找一个谜题的瓶颈步骤,也有很多种方法。你可以直接问自己:“如果要解决这个谜题,有哪些事情是必须要发生的?”,然后从那些事情开始想,注意结合其它的策略。
如果你还是觉得困惑,不妨从一个谜题必须要到达的状态开始想:目标/终点。没错,从终点开始倒推也是一种非常常见的解谜思路,且很多时候比正着推要更有头绪。
策略三:证明高级结论
请不要一看到这么“数学化”的表达就被吓到,我只是实在不知道怎么用最少的词语概括这种思维方式了。
在逻辑解谜游戏中,有时我们会得到比“在这个状态下,这么移动,就能到达另一个状态”更高一级的结论,这些结论通常会为我们对谜题中“什么必须发生”和“什么必须不能发生”提供帮助。
在这方面,我能想到的最简单的例子就是《推箱子》:
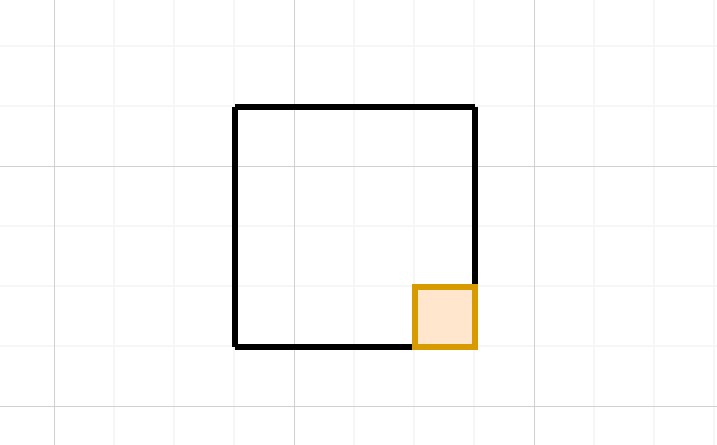
如图,在只考虑普通推箱规则的前提下,当箱子被移动到这样一个角落当中的时候,它就不可能再被移动了,因为玩家只能从上方或左方推动箱子,而箱子的下方和右方又都是墙,阻止箱子的移动。
同理,我们可以考虑如下变体:
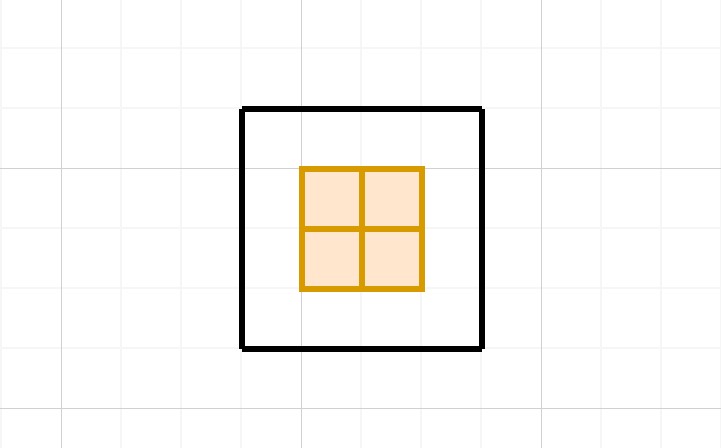
在普通推箱规则中,玩家是不能一次性推动多个箱子的,所以在上面的情况下,四个箱子中的每两个对角箱子都形成了让另两个箱子无法移动的“角落”,因此从整体上来说,这四个箱子的位置已经固定了。
举这个例子是为了说明,对于这样的逻辑结论,将普通的底层推理推广到更广泛的情况也是一种非常重要的思路,这样可以让你“举一反三”,让你可以想象更多类似的情况,比如下面这个情况:
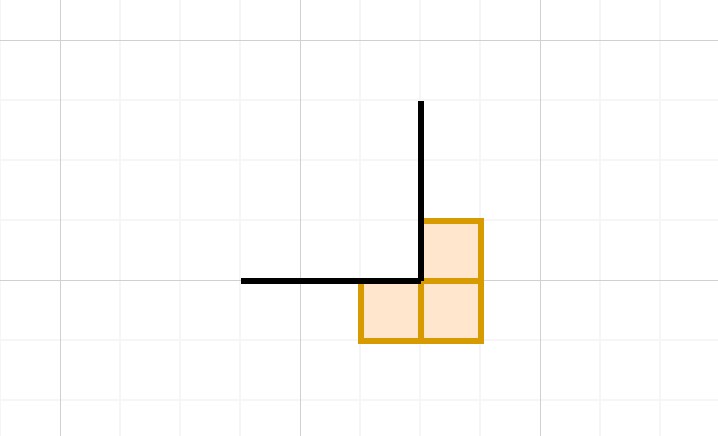
无非就是把上面的情况中的一个箱子换成了墙,并不会影响具体的效果。
通过这样的高级结论来发现什么能做(瓶颈步骤)以及什么不能做(失败状态)可以带来非常高的成就感,但在运用时也需要非常注意如下事项:
你有没有真的“证明”出一个更广泛的结论?该结论是不是只在特定情况或条件下成立?
在新机制/新交互加入后,你的结论是否仍然成立?
如果不多加注意,有可能会因为“伪证”而错过正确的可能性,甚至有可能得出更多根深蒂固的错误结论,最终导致卡关。所以在得出这样的结论之前,一定要谨慎再谨慎。
中场休息
以上就是我目前能想到的主要策略,我只挑了这种大方向来说,如果将话题拓展到各种各样具体的推理方法,那就有点太长了,而且会显得很乱。也欢迎大家在评论区分享自己的见解!
那么接下来,我会举几个具体谜题的例子,用来说明上述这些策略在解谜中是真的有用。
案例一:Microban 1
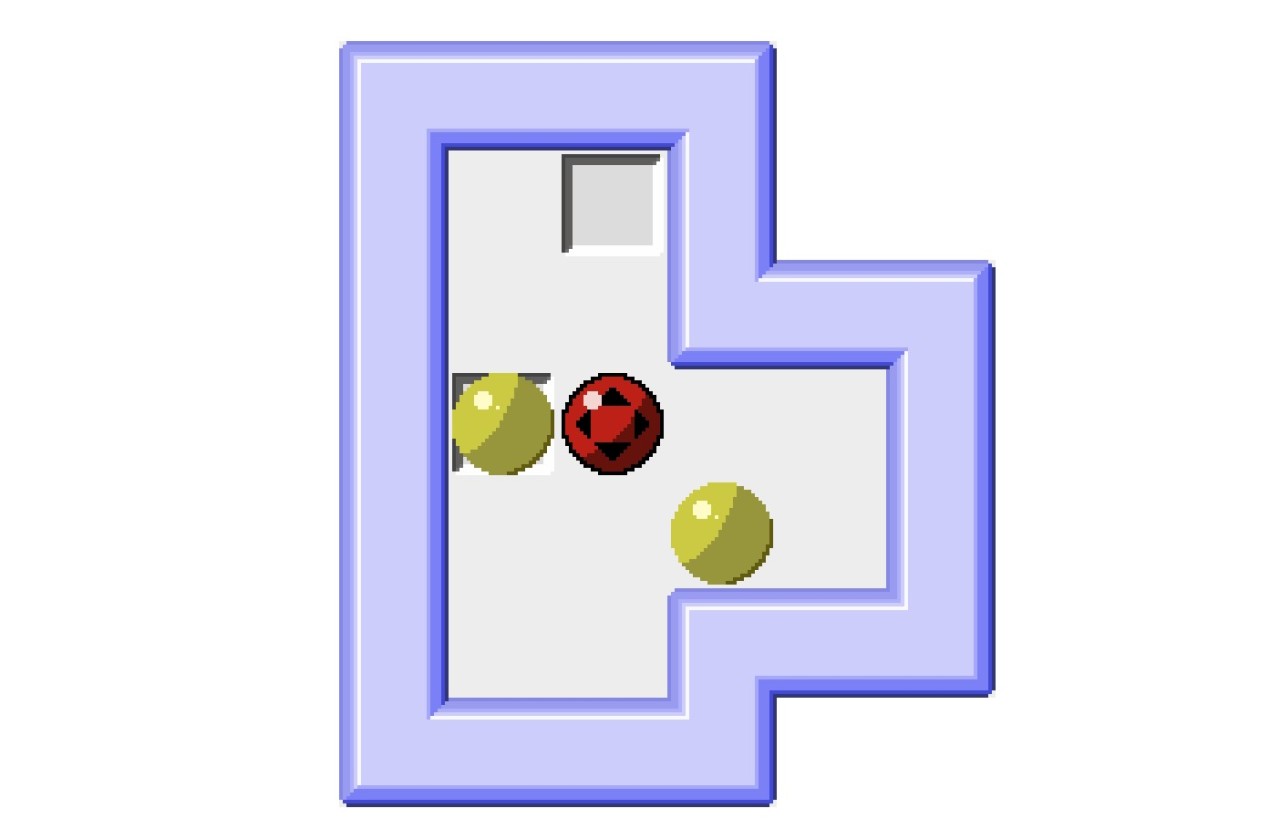
Microban是由David W. Skinner设计的极简纯推箱谜题集(可以在itch.io上搜索),其中的第一个谜题(上面截图中的谜题)已经成为了Thinky解谜圈内的经典梗。在上面的图片中,红色的是可操纵的主角,黄色是“箱子”,而方形的是箱子要被推到的目标。虽然对于推箱老手来说,这个谜题随随便便就可以做出来,但是用它来演示老手背后可能的逻辑过程,我觉得非常合适。
为了方便描述,将目标格和箱子标号如下(易得该状态和上面状态等价,可以互相到达):
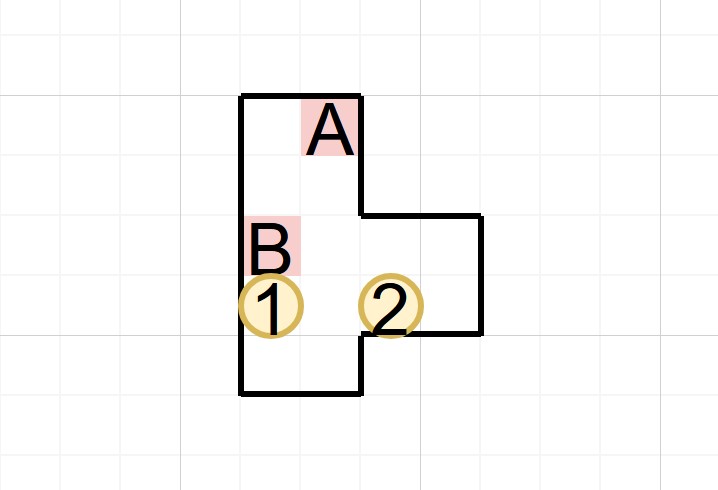
首先我们可以立刻倒推:在最终状态下,两个箱子要分别到达两个目标格,可是每个箱子分别对应哪个目标格呢?利用一个简单的高级结论——箱子1在这种情况下不可能离开左边墙壁——我们可以立刻得到,目标A只能由箱子2来到达(因为箱子1到不了),那显然目标B就和箱子1对应了。
根据这一点,我们进一步发现一个瓶颈步骤:箱子2必须要从右边的凹陷当中出来。它不能往右,因为会卡死在角落里,也不能往下或往上,因为有墙堵着,所以唯一的方式就是往左。在箱子2向左后,它不能向左或向下卡在角落里或者左边的墙上,也不能向右回到本来的位置,要不然刚才那一步就没意义了,因此之后只能向上。
于是具体而言,我们需要先将箱子2向左推,然后几乎立刻将箱子2向上推,让我们具体考虑一下这个情况:
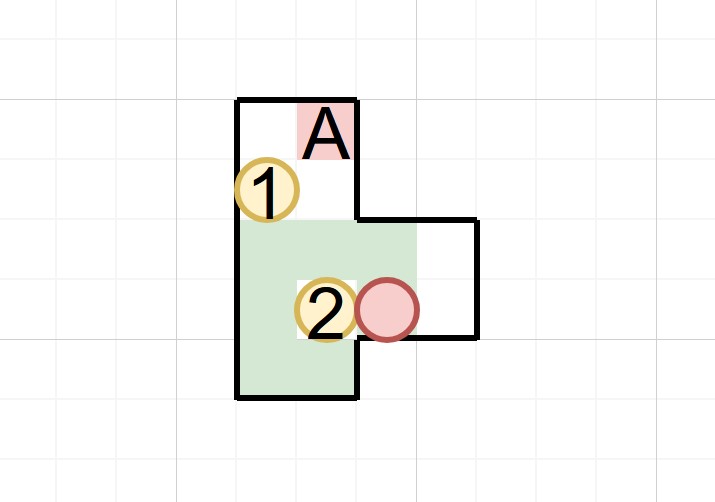
先忽略箱子1的位置,单纯看主角(红色圆)在向左推箱子2之后,又要把它向上推,中间需要经过哪些格子,显然是图中绿色的那些位置。那如果已知这些格被占用、箱子1不能卡在角落、箱子1不能离开左边墙壁所有这些结论,那么箱子1在这个状态下只能有一个可能的位置,那就是上图中箱子1的位置。那么这个瓶颈状态就被完全确认下来了,这个状态必须被经过,而且在将箱子2向上推之后的下一个状态是:
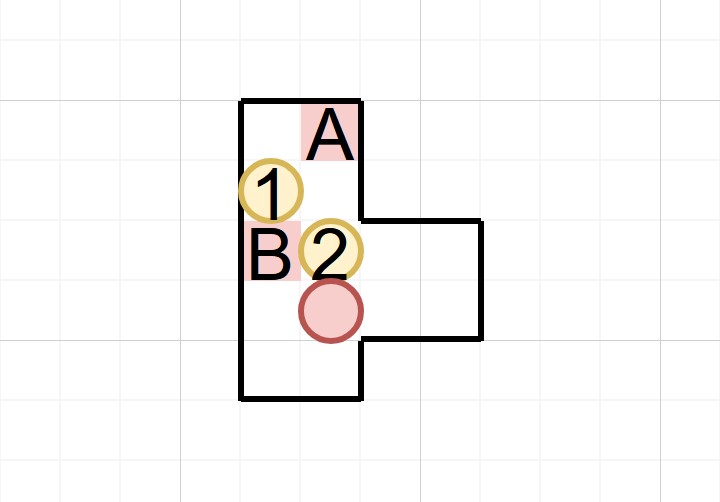
显然,如果箱子2不移动的话,主角只能把箱子1推进角落卡死,那么再考虑其它方向,箱子2最终只能向右再次进入凹陷,但此时已经和之前的状态有本质不同了,不用担心重复。之后就很简单了,把箱子1和2依次推到位即可。
对于推箱老手来说,处理这些逻辑基本上就是一瞬间的事情,我只是把这些逻辑表达了出来,所以看上去很复杂,但只要熟悉这种思考方式,多加练习,不消多时,你也能够成为“推箱大佬”。
接下来举一个更加困难的例子,来自一款我最近刚刚开始玩的解谜游戏:
案例二:Only Sliding某谜题

游戏:Only Sliding
这款游戏出自《Recursed》的作者,据说只包含“滑行”机制,所谓“滑行”机制是指,玩家可以操纵一些块进行移动,但每一次移动,块都会朝这个方向移动到撞上什么东西为止,就像在冰面上“滑行”一样。
根据我目前的体验,这个游戏当中的谜题确确实实就是纯粹的滑块挪移,难度很高,但这并不代表它的谜题设计不好,相反,很多谜题仍然可以通过逻辑推理得到很多有用的结论,减少需要试错的可能性。
这里要举例的是这款作品的一个前期谜题,不在上面的截图中,但如果只是展示题面的话也不涉及什么剧透。为了方便,我直接画了张示意图:
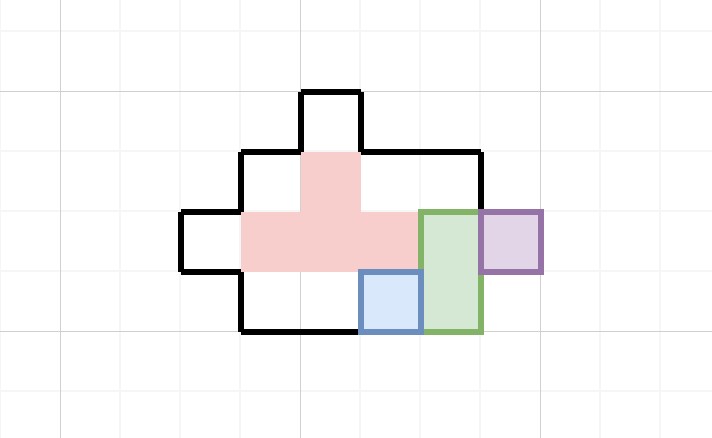
图中的红色部分是过关的目标位置,黑色的边框是不可移动的墙,而右下角的三个不同颜色的块就是要被玩家操纵到达目标位置的几个块,玩家一次只能操纵一个块移动。
首先倒推,显然过关状态是下面这样(两个1x1的块可以互换位置):
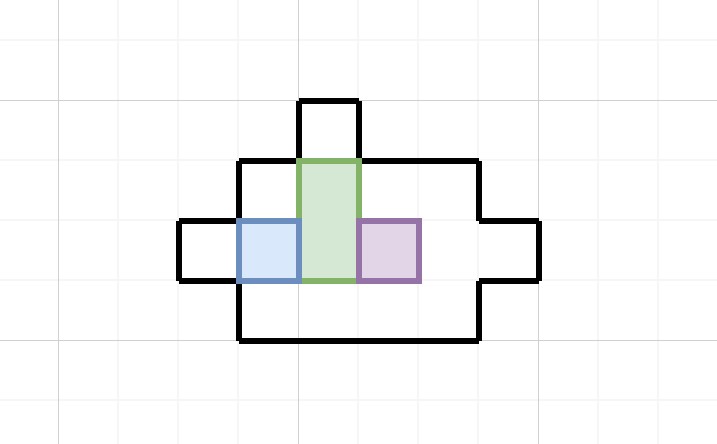
注意到,在过关状态中,两个1x1的块都位于谜题从上到下第三行,但初始状态并不是这样的(蓝色的块在第三行外),所以必须存在一个瓶颈步骤,让两个1x1的块全部进入第三行。第一个1x1的进入有很多方法,但在这里非常值得考虑的是,第二个1x1是怎么进入第三行的。
此时,由于第一个1x1已经进入第三行,那么用它来把第二个1x1垫进第三行就是不可能的,而第二个1x1又显然不可能纯靠自己和关卡边框进入第三行,因此只有一个结论:第二个1x1需要通过垫在1x2的块上进入第三行。
不难发现,1x2块和第二个1x1块在某个瞬间一定会形成下面这个布局(先不考虑第一个1x1块的位置,只需要知道它在第三行就好):
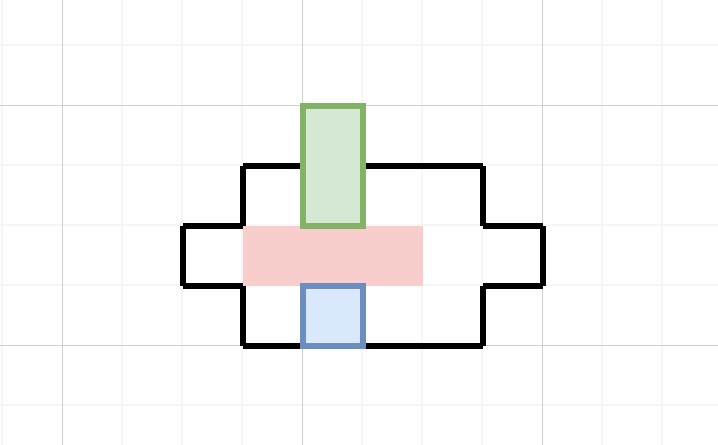
然后1x1的块向上移动,就此进入第三行。这就是关键的瓶颈状态。
那么现在先考虑怎么到达这个瓶颈状态,我觉得这是这个谜题里最难的部分。将这个状态看作目标状态,我们可以再次倒推:在来到这个状态之前,上一步是哪个块在动?
已经在第三行的1x1块不可能,因为就算能动,它也只能在第三行来回动,对我们的分析没有帮助;有没有可能是另一个1x1块呢?如果1x2块已经在现在这个位置,另一个1x1块在第三行,那么这个1x1块不可能被垫到这一格,除非从上面一格往下,但那个状态反倒是我们最终要到达的状态,这样做是倒反天罡,所以不行。那么就只剩一个可能:上一步移动的是1x2块,而且是从下往上移动进上面的凹陷的。
再往回推,你会发现这一步的再上一步,动的也必须是1x2这个块,而且是向左/向右到达这个位置的,那么此时,已经在第三行的1x1必须负责垫住它,那么这个块的位置应该在哪里,我们心里就有数了。就这样一步一步往回推,具体情况具体分析,外加合理范围内的尝试,就可以得到一条非常夸张的逻辑链条。如果你想要确认一下,下面是之前最近的一个瓶颈状态:
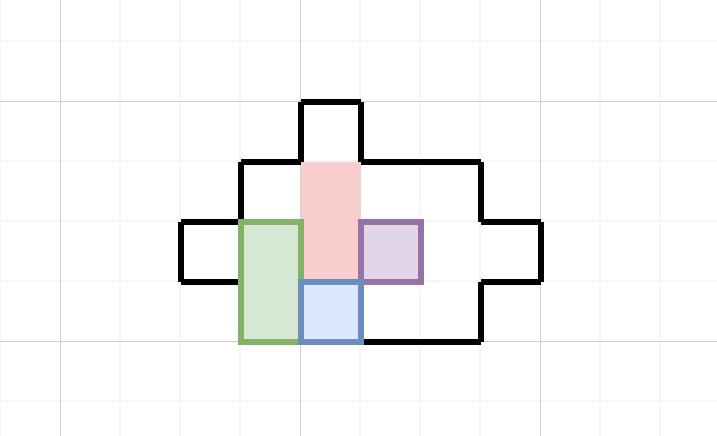
从这个状态开始移动1x2的块就可以到达上面的状态。再往前我就不举例了,大家应该已经明白意思了。而从最一开始的瓶颈状态开始,如何到达最终状态,也可以使用类似的思路解决。这个阶段的核心问题是如何让1x2在纵向上到达正确的位置,而既然两个1x1块都已经在第三行,那就不可能拿它们来垫住上面或者下面,所以只能通过墙壁到达正确的纵向位置,然后再横向垫到1x1块上,这里我就不再赘述了。
这样的谜题正是因为只有这么一条由各种各样的“瓶颈状态”连接而成的前进道路,所以如果纯纯靠试,基本是不可能做得出来的。除非你大脑爆算能力真的非常强(
结语

游戏:Lab Rat(即将发售)
如果想的话,我还可以举出好多好多的例子,不管是不是推箱子,但现在就到这里吧,如果大家还感兴趣的话,我也可以试试找找其它例子进行分享哈哈
虽然必须要说的是,并不是所有逻辑解谜游戏都“支持”这样的逻辑思考方式,但我觉得优秀的谜题设计不仅仅要做到“有解”,也不仅仅是要做到“很难靠试解出”,而且还要做到“有迹可循”,而其中的一种方式就是鼓励这种有趣的思维方式:有关空间位置、时间顺序等的逻辑推理。当然,不一定需要是这么严谨的逻辑推理,只要能在某种程度上有“可解释性”即可。在以这种思路为核心开发的解谜游戏之中,通过逻辑推理来解决谜题不仅会让你感到如鱼得水,而且这种靠自己解谜的成就感还能再上一层。
而对于那些认为“这一大堆东西有什么意义?”或者“玩个游戏还要这么累?”的玩家,我并不打算反驳,所谓“意义”和玩游戏所寻求的“价值”本来就是因人而异,解谜游戏就是这么一个需要主动找到乐趣的品类,如果你觉得这太麻烦,那不玩就好了。并不是说玩解谜的玩家智商就比不玩解谜的玩家更高,或者解谜游戏的价值就一定高于其它游戏的价值。如果你有看到有解谜玩家表现出这样的“优越感”,请你清楚我和绝大多数Thinky解谜社区玩家都不认同这样的行为。
不过,我还是很希望我的这些文字能够为更多对解谜感兴趣,但是却苦于没有系统的思维方法的玩家,提供那么一些帮助。
那么就说到这里,我们下次有缘再见!
无奖竞猜:从我这篇文章的用词来看,你可以猜一猜我是学什么的,我觉得非常好猜了吧哈哈哈
更多游戏资讯请关注:电玩帮游戏资讯专区
电玩帮图文攻略 www.vgover.com













