目录
1 游戏数值的基本设计方法
1.1 搭数值框架的方法
1.2 推数值细节的方法
2 RPG数值——成长
2.1 成长标杆
2.2 战斗属性成长
2.3 战斗属性分配
2.4 细化成长
3 RPG数值——战斗
3.1 伤害公式
3.2 战力公式
3.3 职业设计
3.4 怪物设计
3.5 战斗测试
4 RPG数值——经济
4.1 资源流转结构
4.2 消耗模型
4.3 产出模型
4.4 价值体系
写在前面:
笔者阅读了《游戏数值百宝书》、《平衡掌控者》、《游戏数值设计》、《游戏策划工作手册》四本和游戏数值相关的书,浏览了多个网络平台上大量与游戏数值相关的文章,发现不同公司不同策划的建表步骤和计算方法差异很大,造成差异的原因是大家所用的数值模型是不统一的,每个人都有自己的惯用模型和建表习惯,这对于刚接触游戏数值的新人(比如我)来说并不友好。
但读得多了就会发现,虽然具体细节上的算法和公式存在差异,细节背后的设计目的和设计思路却是一致的。这也很容易理解,因为大家要解决的问题是类似的,故而摸索出来的方法也都殊途同归。本文基于自己的思考梳理了一下RPG数值共通的设计思路,希望能对和我一样刚开始学习游戏数值的小伙伴有些许帮助。有不对的地方欢迎评论或者私信讨论和指正,希望问题说得具体一些,多谢大家。
需要强调的是,数值策划的工作分为“建”和“调”,前期把表建出来,中后期反复测试和调数。“建”更多的是技能上的东西,而“调”则需要大量的游戏阅历和工作经验做支撑。本文梳理的是与“建”相关的核心设计思路,并不包含调数的内容。此外,文中的例子主要来自游戏《原神》,所有与《原神》相关的图表都只是笔者自己的粗略反推,不代表真实数据。
1 游戏数值的基本设计方法
1.1 搭数值框架的方法
对于原创玩法和成熟玩法,搭数值框架的方法有所差异:
对于创新型原创玩法:搭建简易系统进行快速迭代,即,根据核心玩法确定属性框架→给出具体公式→验证体验→调整核心玩法及属性框架→进行新一轮迭代。
对于有成熟原型的玩法:找到市面上的同类型游戏,反推其数值架构和数值细节→分析其设计目的和实际效果→根据自己的项目特点对已有的框架做调整。
由于数值会多次调整,搭框架时可以采取一些能提高效率的建表习惯:
把每个excel的首页作为参数页,或者在每个页面的顶部设置一个参数区,把需要手填的参数单独放在参数页或参数区中,其他版块从这里引用,方便后续调参。
设置一个控制数值量级的参数,做表的时候给所有相关数值乘上这一参数,方便后续随时对数值的量级做调整。
用excel里的“数值验证”功能设置单元格的填写限制,对于该功能实现不了的需求随手编写检查函数,避免后续改数时出现错误。
在做概率分配时(要求概率总和为100%,比如将属性分配给养成渠道、将产出分配给玩法模块等),用权重而非直接用概率,方便后续调整。
…
1.2 推数值细节的方法
建表的核心就是根据各种设计需求反推数值细节,数值推导的一般步骤如下:
STEP1明确求解对象:找到能够撑起数值体系的关键参数,将其作为求解对象。
STEP2明确设计需求:设计需求即一些关系到玩家体验的基础参数的值,也可能指一些特殊的设计要求,每个设计需求都会对求解对象产生一定的约束。比如在设计属性投放比例时,“生存时长=20s”就是一个需要满足的设计需求。
STEP3求解:根据第二步中的设计需求反推出第一步中的未知参数。如果约束条件个数少于参数个数(存在无穷多个解),可以拍脑袋给出部分未知参数的值然后求解其他未知参数的值,只要满足设计需求就行。
在设计有递增趋势的数值时(如属性成长等),需要根据变量之间的关系确定曲线的形状,下面列举了一些常用的曲线类型:
线性:一次函数
边际效应递增:高次幂函数(指数>1,最常用的是二次函数),指数函数(底数>0)
边际效应递减(无趋近):低次幂函数(指数<1),对数函数
边际效应递减(趋近):指数函数(底数<0),反比例函数(x/(x+a))
注:确定曲线类型时尽量不要使用太过高深的数学,对程序来说负载太大,容易跑不动,最好只用加减乘除和min/max,然后通过不同的参数取值来实现不同的效果。此外,为了在不同游戏阶段保证不同的游戏体验,实际游戏中大都采取分段函数的形式,由于玩家对小数值比较敏感,游戏前期要抠得细一点,多分几段,必要时可以放弃使用公式,每个点都当作特殊情况来手填,后期数值变大且影响因素变多,玩家逐渐不敏感,再用公式。
在设计包含概率的数值时(如强化/合成等养成数值、掉落/抽奖等产出数值、暴击/闪避等战斗数值),为了防止玩家流失,需要控制极端负面概率的出现,下面列举了一些常用方法:
让概率不断增加:如果本次不中,下一次增加固定大小或固定比例的概率,初始概率和每次增加量的取值可以根据设定的最多中奖次数和平均中奖次数来反推。例如原神的抽卡概率就是采用这个方法,角色池五星概率为0.006,自74抽开始每抽增加0.06的概率,第90抽时设定概率为1。
把概率变成频率:有两种方法可以把概率固定为频率,一是预存结果的方法,如果概率是5%,60次保底,则就在1-60中随机抽3个数作为中奖次数,如果概率不变,改为100次保底,则就在1-100中随机抽5个数作为中奖次数。把概率变成频率进行预存后,随机性不复存在,可以有效避免玩家通过读档反复赌概率。二是计数器或奖金池的方法,当有人杀怪或有人抽奖时计数器加一,如果概率是千分之一,则杀到第1000只怪时或抽到第1000次奖时掉落,同时计数器归零。也可以给不同的怪或不同的奖券设置不同的权重,计数器每次加的数不一样,杀掉首领怪的人或用优质奖券抽奖的人更容易把计数器顶满。该方法常用于大型MMO的稀有物品掉落,优点是可以完全通过刷新频率控制服务器中稀有物品的产出数量。
2 RPG数值——成长
RPG游戏中玩家的各方面能力会不断成长,成长数值的设计目的就是把玩家各方面的成长量化出来,同时把玩家的成长速度规划出来。设计思路如下:
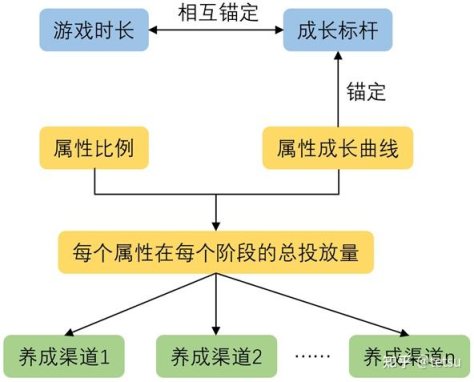
STEP1:选定成长标杆,规划整体成长节奏。这一步的设计目的是利用成长标杆把玩家的成长与游戏时长联系起来,后续设计其他成长板块时,锚定成长标杆就相当于锚定了游戏时长,从而能让玩家按照提前设计好的节奏来成长。
STPE2:确定战斗属性有哪些,设计属性投放比例及属性成长曲线。战斗属性是RPG的核心属性,这一步的设计目的是确定每个战斗属性在每个成长阶段的总投放量。
STEP3:确定养成渠道有哪些,规划每个属性在每个渠道的投放比例。这一步的设计目的就是把第二步中规划好的总投放量分配到不同的养成渠道中去。
STEP4:细化每个养成渠道的成长数值。根据前几步中的规划把表拉出来。
2.1 成长标杆
成长标杆用于锚定游戏时长,其他任何关乎游戏节奏的板块(属性成长、内容投放、资源投放等)都锚定等级,从而也锚定了游戏时长。
最常见的成长标杆是角色等级,根据世界观不同还可以将角色等级包装成其他形式,比如《斗战神》的修炼年数,《千年》的年龄等。
选定等级作为成长标杆后,需要规划每个等级升级所需的游戏时长(小时或天),具体思路参照1.2中的三个步骤:
STEP1明确求解对象:一般来说每级耗时应该是逐步递增的,可以采取几级一个跳变的方式递增,也可以采取一次函数或二次函数递增。要求解的对象就是函数中的未知参数。
STEP2明确设计需求:每级耗时需要满足的设计需求是已设定的游戏生命周期、首日等级、首周等级、首月等级等。
STEP3求解:根据已设定的游戏生命周期、首日等级、首周等级、首月等级等条件反推函数中的未知参数。
以《原神》为例,由于《原神》中角色的养成方式是混合式养成(既有横向收集要素也有纵向数值要素),一个玩家可以快速养成多个角色,因此用作成长标杆的并不是角色等级,而是冒险等级。
假设普通玩家每天只玩1小时,不使用脆弱树脂(每天消耗180点树脂),游玩内容是每日委托+4个宝箱+60个大世界物产+1次藏金之花+1次启示之花+1次武器秘境+1次天赋秘境+1.5次圣遗物秘境+40个普通小怪+20个精英怪+1个首领怪+1个周boss,则该普通玩家的升级耗时如下图所示(笔者自己的粗略反推,不代表真实数据):
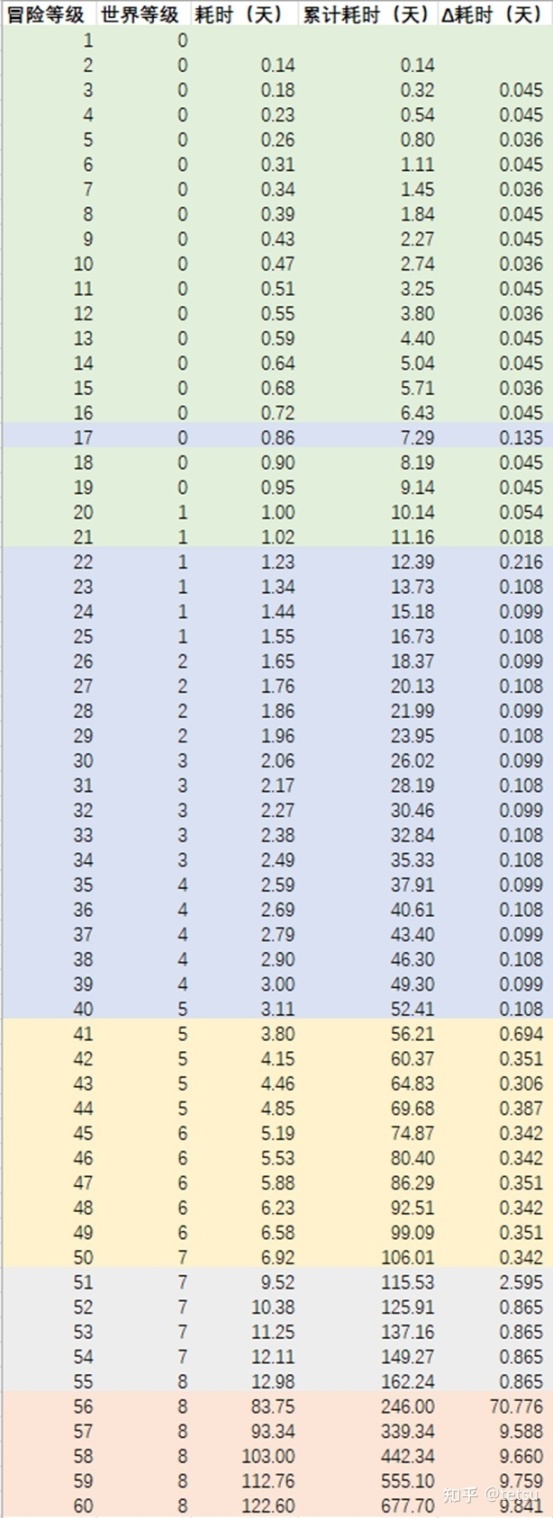
可以看到,《原神》的耗时曲线是“分段线性+加速递增”的,升级耗时=a+b*等级,但每隔5-10个等级参数a和b都会发生一次跳变,“Δ耗时(天)”一列其实就是参数b的取值,上表中每次变色,就是参数a和b发生了跳变。
2.2 战斗属性成长
注:在一些书里,规划属性成长用的是力量、智力、灵巧等基础属性,但个人认为用战斗属性更好,因为除角色外的所有养成渠道养成的都是战斗属性,用基础属性的话后续分配属性时还需要再转化一次,相对比较麻烦。
RPG的战斗属性可以分为以下几类:
核心战斗属性:攻击力、防御力、生命值上限,即攻防血铁三角,是RPG必不可少的属性。
高级战斗属性:高级战斗属性可以分为攻击类、防御类和生命类三类,主要设计目的是丰富伤害计算的机制,增加战斗系统的深度,为战斗增加惊喜感。每个游戏的高级战斗属性不尽相同,取决于该游戏的战斗设计。以《原神》为例,《原神》中的高级战斗属性有:元素精通(攻),暴击率(攻),暴击伤害(攻),某元素伤害加成(攻),物理伤害加成(攻);护盾强效(防);某元素抗性(防),物理抗性(防);治疗加成(血),受治疗加成(血)。
速度类战斗属性:影响DPS分母的战斗属性,在RPG中的重要程度不高,大都是隐性属性(不显示在面板上的属性)。以《原神》为例,《原神》中的速度类战斗属性有:攻击速度;冷却缩减,元素充能效率;移动速度,体力上限。
设计成长数值时只需要规划出标准人的战斗属性成长即可,后续战斗数值模块在设计不同职业和不同怪物时,会以这里的标准人为基准。规划战斗属性成长一般分两步,第一步确定属性投放比例,第二步确定属性成长曲线。第一步给出战斗属性的总投放量,第二步给出成长标杆每一级所对应的战斗属性投放量。
属性投放比例:
参照1.2中给出的三个步骤:
STEP1明确求解对象:各个战斗属性总投放量之间的比例关系。
STEP2明确设计需求:约束属性投放比例的设计需求主要是生存时长和免伤率。1)生存时长:战斗中最重要的指标,双方的生存时长反映了战斗的胜者,也间接反映了角色的战力。假设两个标准人互殴,通过对生存时长的设计要求,能够确定血量与伤害之间的数值比例。2)免伤率:如果伤害公式(关于伤害公式的介绍参见3.1)是乘法公式的话,确定属性投放比例时可以不考虑免伤率,因为通过调参数就能将免伤率控制在任意范围内。如果是减法公式的话,则需要通过对免伤率的设计要求来确定攻防之间的比例关系。
STEP3求解:不妨设攻击力为1,则1)如果伤害公式用乘法公式:拍脑袋确定其他攻击类属性与攻击力之间的比例关系→根据伤害公式和已经设定的免伤率算出伤害→根据已经设定的生存时长推出血量与攻击力之间的比例关系。乘法公式下防御力可以看作是单独的体系,攻防之间的比例可以随意设定。2)如果伤害公式用减法公式: 拍脑袋确定其他攻击类属性与攻击力之间的比例关系→根据已经设定的免伤率推出攻击力与防御力之间的比例关系→根据伤害公式算出伤害→根据已经设定的生存时长推出血量与攻击力之间的比例关系。
《原神》的属性投放比例比较特殊,“标准人互殴的生存时长”这一设计需求对于《原神》来说并不重要,实际上,如果原神中的两个输出型角色互殴,生存时长只有不到3s,这看似很不合理,但放在《原神》中却是合理的,原因在于《原神》是纯PVE游戏,标准人互殴的生存时长并不能反映实际战斗情况,实际上,为了覆盖更加广泛的玩家群体,《原神》中的角色数值对于玩法是明显溢出的,玩家的血防数值应对攻低血高的怪物绰绰有余。此外,《原神》是团队作战,玩家实际拥有的其实是四个角色的血量,团队中还存在能力突出的盾辅奶辅,整个队伍循环起来后基本不存在生存问题。
属性成长曲线:
战斗属性的投放有两种方式,一种是连贯的,一种是阶段性的(在某几个节点集中投放)。连贯的投放对应纵向数值型的养成方式,阶段性的投放对应横向收集型的养成方式。
核心战斗属性(攻防血)是连贯投放的,一般为线性递增,后期由于升级耗时变长且玩家逐渐麻木,可能需要通过一些跳变实现加速递增(例如,1-50级每级提高90点攻击力,50-100级每级提高180点攻击力)。
高级战斗属性可能是连贯投放的,也可能是阶段性的,一般为加速递增,越后期的节点投放的量级越大,从而给玩家提供指数级增强的数值刺激。
《原神》中最主要的三个养成渠道(角色、武器、圣遗物)都是混合式的,既有纵向数值的元素也有横向收集的元素。前期资源少,可收集的角色/武器/圣遗物也较少,养成更偏纵向,主要靠升级来进行缓慢的线性提升;后期随着玩家的资源越来越多,角色/武器/圣遗物基本收集到就能拉满,养成更偏横向,主要靠收集来进行阶段性的大幅增强,强力角色/武器/圣遗物的加入大大拔高了基础数值,不同系别角色的加入则丰富了可利用的元素反应,使玩家能够更游刃有余地面对不同环境。
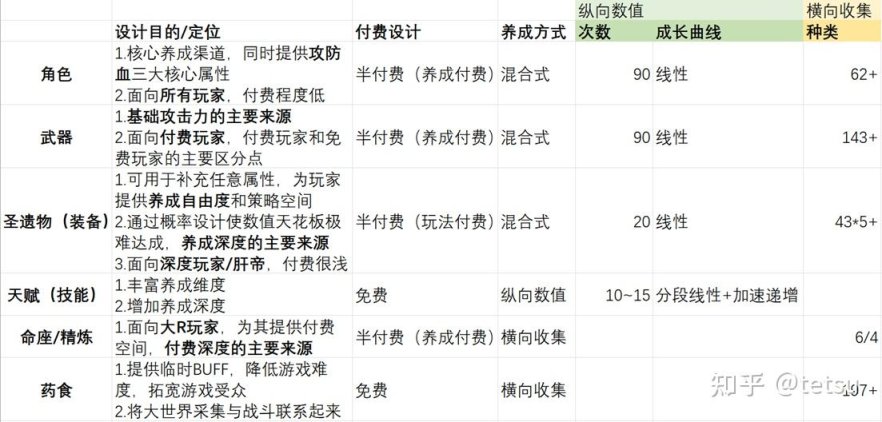
注:表中的“+”表示随着版本更新,可收集的种类还在不断增加。
在做好养成规划后,把属性成长按照百分比分配给不同的养成大类,然后在养成大类内部再进行二次或三次分配。分配时要参考每个养成渠道的重要程度,比如规划时希望玩家喜好的优先级是A渠道>B渠道,在分配时就要给A分配更多的比例,此外也要把A渠道做得更加外显、更加简单、随机性更小,方便玩家认知和感受。
同样以《原神》为例,以极限投放(指投放至游戏中的所有属性点,不考虑可获得性)为标准进行统计,属性分配比例大致如下图所示(笔者自己的粗略反推,不代表真实数据)。可以看到,基础生命值、基础防御力、某元素伤害加成、治疗加成四个属性主要来自角色和圣遗物;基础攻击力、物理伤害加成两个属性主要来自武器和圣遗物;其他属性的主要来源都是圣遗物。这印证了上文的推测(圣遗物是养成深度的主要来源),玩家如果想堆什么属性实现毕业的话,还得在圣遗物上下功夫。

极限投放不考虑可获得性,事实上玩家在通过养成获取属性点时面临着诸多限制,一个角色只能有一个副属性,一个武器只能有一个副词条,圣遗物只能戴五个,圣遗物副词条的位置和强化次数都有限,这就使得《原神》中毕业角色的属性分布跟上表大不相同。对于这种包含大量自选的养成,在估计真实投放比例时可以先评估该养成渠道所包含的隐性引导,即,策划希望玩家去追求哪个属性、哪个属性的实际收益最高。对不同职业和不同流派的玩家来说实际收益高的属性不尽相同,此处以输出类角色为例,角色和武器的副属性分别选暴击和暴伤,圣遗物在提供大量双暴词条的同时提供少量的其他属性,一个典型输出角色的实际属性分布大致如下图所示(笔者自己的粗略反推,不代表真实数据):

根据2.2中的分析,《原神》作为纯PVE游戏,角色数值对于玩法是明显溢出的,非自选的养成所提供的血防属性已经足够,再加上强悍的盾辅奶辅,基本不存在生存问题。因此玩家的选择往往是把可自选的养成都用来提升攻击类属性,力求快速杀怪。由于玩家基本只追求DPS,输出类角色堆双暴,增伤类角色堆双暴和元素精通,除了某些奶妈要稍微堆一下治疗加成外,防御类、生命类属性基本无人问津。策划解决这一问题的方式主要是转模,即,让技能倍率乘上别的属性而非面板攻击力,从而把该属性转化为攻击伤害,目前《原神》中生命转模的角色有胡桃,防御转模的角色有荒泷一斗、阿贝多。
2.4 细化成长
在完成前三步之后,成长体系的框架已经搭好,下一步要做的就是把具体的数拉出来。
首先用对标成长标杆的方法得出每个养成渠道在每个阶段的战斗属性投放量:对于横向养成,把不同物品的投放节点和成长标杆对应起来;对于纵向养成,把该养成渠道的等级与成长标杆对应起来。由于战斗属性成长和渠道等级同时对标了成长标杆,可以用成长标杆将二者联系起来,即,某渠道在某阶段的某战斗属性投放量=该战斗属性在对应成长阶段的总投放量*该战斗属性在该渠道的分配比例。
其次,如果该养成渠道有自己的一套属性,还需要设计属性转化公式并进行逆推。例如,在很多RPG中,角色这一养成渠道往往不直接养成战斗属性,而是养成力量、智力、灵巧等基础属性,然后通过属性转化公式将其转化为物攻、魔攻、攻速等战斗属性。在这种情况下就需要把分配给角色渠道的战斗属性还原为基础属性。
3 RPG数值——战斗
3.1 伤害公式
伤害计算公式的作用是结合攻方的攻击类属性值和守方的防御类属性值计算出攻击造成的最终伤害。伤害计算公式可以分为减法公式和乘法公式两大类:
减法公式:伤害=攻击-防御。
此处的“攻击”指的是所有攻击类属性放在一起计算后的结果,“防御”指的是所有防御类属性放在一起计算后的结果。如果伤害公式用减法公式的话,“攻击”和“防御”一般会用加法来计算:攻击=角色攻击+武器攻击+技能攻击+…,防御=角色防御+装备防御+…。
设h表示伤害harm,a表示攻击attack,d表示防御defense,则减法公式可以表示为h=a-d,h'(d)=-1<0,h''(d)=0,伤害随着防御的增大而减小,堆防御的边际收益不变。
减法公式的优点是方便玩家理解,仅靠心算就能直接算出伤害,缺点是堆防御的边际收益不变,玩家可能会大量堆防御导致不破防。1v1的不破防很难解决,但1vN的不破防可以通过“防御力随围攻人数的增加而衰减”的方式解决。
乘法公式:伤害=攻击*(1-免伤率),其中免伤率=防御/(防御+参数表达式)。
此处的“攻击”指的是所有攻击类属性放在一起计算后的结果,“防御”指的是所有防御类属性放在一起计算后的结果。如果伤害公式用乘法公式的话,“攻击”和“防御”一般会用乘法来计算:攻击=(角色攻击+武器攻击)*(1+技能作用百分比)*(1+装备增伤百分比)*…,防御=(角色防御+装备防御)*(1+技能作用百分比)*…。
设h表示伤害harm,a表示攻击attack,d表示防御defense,dr表示免伤率defense rate,pe表示参数表达式parameter expression,则免伤率公式可以表示为dr(d)=d/(d+pe),伤害公式可以表示为h=a*(1-dr(d)),该式有如下性质:
dr<100%,dr'(d)>0,h'(d)=-a*dr'(d)<0:免伤率随着防御的增大而增大,逼近100%,伤害随着防御的增大而减小,逼近0。实际游戏中一般不会让免伤率真的去逼近100%,而是会通过控制防御类属性的最大投放使其逼近一个小于100%的临界值,一般为60%或75%,这能够避免不破防的问题,保证至少40%或25%的伤害。
dr''(d)<0,h''(d)=-a*dr''(d)>0:免伤率对临界值的逼近是边际递减的,随着防御力的不断增加,伤害的减小幅度越来越小,堆防御的边际收益递减,这能够促使玩家更加均衡地堆属性。
pe可以是常数也可以与攻方等级、守方等级、攻方攻击力等变量相关,下面举几个例子:
在游戏《英雄联盟》中,pe为常数。此时会出现一个有趣的性质:有效生命值随防御的增加而线性增长。原因是有效生命值=实际生命值/(1-免伤率)=实际生命值/(pe/(d+pe))=实际生命值*(1+d/pe),pe取100的话防御其实就是守方额外获得的生命值加成百分比。
注:有效生命值(Effective HP,EHP)指实际生命值加上守方所有防御类属性(防御、躲避、格挡、抗暴击等)提供的等价血量。EHP=角色生存时长*(攻击力*攻击速度)=(实际生命值/(攻击*(1-免伤率)*攻击速度))* (攻击力*攻击速度)=实际生命值/(1-免伤率)。
在游戏《原神》中,pe与攻方等级相关,PE=a*攻方等级+b。设l1表示攻方等级,dr'(l1)<0,h'(l1)=-a*dr'(l1)>0,在防御不变的前提下,攻方等级越高,越能造成更大的伤害。在这一公式下,游戏中存在等级压制,这能够制造出更强的成长感,比如《原神》中的世界boss,一开始等级远高于玩家,压迫感极强,后期却不堪一击。
在游戏《魔兽世界》中,pe与守方等级相关,PE=a*守方等级+b。设l2表示守方等级,dr'(l2)<0,在防御不变的前提下,守方等级越高,免伤率越低。在这一公式下,玩家等级越高,越要继续堆防御(不堆的话实际防御力就会自动降低),从而给玩家提供了一个长线追求的点。
在游戏《暗黑破坏神》中,pe与攻击相关:PE=a*攻击+b。对于上述其他公式来说,h''(a)=0,堆攻击的边际收益不变。但对于该公式来说,h''(a)>0,伤害随着攻击的增加而加速增长,堆攻击的边际收益递增。这有利于攻击方,常用于单机割草类PVE游戏,对于PVP游戏不友好,会放大玩家之间的差距导致角色生存时长不稳定。
从上面的分析中可以看到,不同的公式有不同的应用范围,总结一下就是:
减法公式和pe包含攻击的乘法公式做PVP会导致一些问题,一般都是做PVE,其中,减法公式适合比较硬核的PVE,pe包含攻击的乘法公式适合割草类爽游。
其他乘法公式做PVE和PVP效果都很好,其中,弱养成的PVP游戏pe取常数就行,重养成又包含PVP的RPG一般会让pe与角色等级相关联。
注:实际游戏中可以混合使用多种公式,比如在传统RPG中,物理攻击多为近战,技巧性强/不好躲,可以用减法公式,提高物防的收益让玩家重视物防;法术攻击多为远程,比较好躲,可以用乘法公式,让玩家重视躲闪技巧而非靠法防硬上。
在一些游戏中,为了避免玩家进行一些和设计目的不符的行为,或者为了突出该玩法的设计特色和目标体验,会对基础的伤害计算公式进行一些调整,调整的方法是对玩家与目标数值之间的偏离进行惩罚:怪对玩家造成的最终伤害=原伤害*(1+f),f表示f((目标数值-玩家数值)/目标数值)或f(目标数值-玩家数值),前者惩罚的是相对偏离,后者惩罚的是绝对偏离。公式里的目标数值取决于设计目的,对于考验玩家的输出能力的玩法,目标数值可以取目标攻击力;对于考验玩家生存能力的玩法,目标数值可以取目标防御力…为了防止玩家越级打怪,目标数值还可以取怪物等级。
此外,在一些游戏中,为了给玩家提供战斗的惊喜,会让伤害在适当的范围内进行浮动,浮动的方法是添加两个参数——最大伤害系数和最小伤害系数,每次用伤害计算公式算完伤害后,在原伤害*最小伤害系数与原伤害*最大伤害系数之间随机取一个数作为最终伤害。
下面以《原神》为例看一下实际游戏里的伤害计算公式。如下图所示,《原神》采用乘法公式,共有七个乘区,前五个乘区用于计算“攻击”,后两个乘区用于计算“防御”。

① 面板攻击力=基础攻击力+攻击力加成,基础攻击力=角色攻击力+武器攻击力,攻击力加成=圣遗物主副词条里的攻击力+基础攻击力*攻击力百分比。部分角色(胡桃、一斗、阿贝多)的部分技能存在生命值上限或防御力转模的情况,这种情况下该乘区用的是生命值上限或防御力而非攻击力。
② 直接乘上对应的技能倍率就行,需要注意的是,对于落在该区的增伤类技能(如云堇的飞云旗阵),需要在“前台角色面板数据*前台角色技能倍率”的基础上加上“增伤角色的面板数据*增伤技能的倍率”。
③ 增伤百分比=某元素伤害加成+物理伤害加成+其他伤害加成。其他伤害加成可能来自命座、武器特效、圣遗物特效、落在该区的增伤类技能(如莫娜的星异)。
④ 该公式是根据期望伤害得出的,未暴击伤害*(1-暴击率)+未暴击伤害*(1+暴击伤害)*暴击率=未暴击伤害*(1+暴击率*暴击伤害)。
⑤ 增幅反应总倍率=增幅反应基础倍率*(1+元素精通加成+其他增幅反应加成)。增幅反应基础倍率在后手元素克制先手元素时取2,在先手元素克制后手元素时取1.5。增幅反应元素精通加成=2.78*元素精通/(元素精通+1400)。
⑥ 一般情况下抗性免伤率=抗性;当抗性>75%时,为了防止不破防的情况出现,抗性免伤率=抗性/(25%+抗性);当抗性<0时,为了控制减抗的超额收益,抗性免伤率=抗性/2。
⑦ 防御免伤率=守方防御力/(守方防御力+5*(攻方等级+100)),怪物防御力=5*(怪物等级+100)*(1-减防百分比)。从公式中可以看到,当角色等级等于怪物等级且不存在减防时,防御免伤率=50%。
《原神》中的元素反应除了增幅反应还有剧变反应,增幅反应体现的是一种相互排斥的克制关系,因为克制所以造成了超额的攻击伤害;而剧变反应体现的则是一种环境交互,反应作为第三方主体对场上对象产生伤害。剧变反应伤害的公式如下:
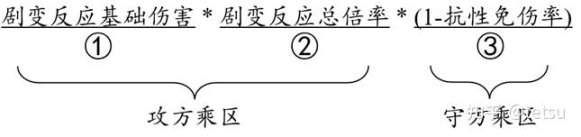
① 剧变反应基础伤害锚定角色等级,曲线关系是“分段线性+加速递增”。
② 剧变反应总倍率=剧变反应基础倍率*(1+元素精通加成+其他剧变反应加成)。剧变反应基础倍率是:超导1,扩散1.2,感电2.4,超载4,绽放4,超绽放6,烈绽放6。剧变反应元素精通加成=16*元素精通/(元素精通+2000)。
3.2 战力公式
战力由生存时长反映,生存时长由战斗属性、技能属性(技能的规则设定,如增伤、闪现等)、玩家操作这三个因素决定,由于玩家的操作水平参差不齐,设计数值时一般只讨论角色战力,战斗公式也只包含战斗属性和技能属性这两个影响因素。
战力的计算可以分为两步,第一步把无法纳入伤害公式的技能属性转化为APS或EHP,思路是先拍脑袋定加成比例,形成一个加成比例表,后续不断通过测试来调整这张表,并连带修正所有影响到的技能。第二步根据战力公式计算出角色战力。
注:DPS一般指每秒造成的伤害,DPS=伤害*攻击速度=攻击*(1-免伤率)*攻击速度;这里新定义一个APS(attack per second)来表示每秒输出的攻击量,APS=攻击*攻击速度。
将无法纳入伤害公式的攻击类技能属性转化为APS:
注:CD时间有很多种不同的计量方式,这里假设技能一经释放CD就开始转。
增伤:假设该BUFF能在技能持续时间内增伤a%,则ΔAPS= 原APS*a%*min{持续时间/CD时间, 1}。一般来说BUFF类技能的ΔAPS会略高于直接伤害类技能,原因是在对方血量较少的情况下,放直接伤害类技能可能会造成秒杀,而放BUFF类技能对方却有可能被队友救下。故需要再给一个加成比例,ΔAPS=原APS*a%*min{持续时间/CD时间, 1}*(1+加成比例)。
减抗:先把减抗转化成增伤,再用增伤的公式。
硬控(目标被控后不能进行任何行动):技能持续时间内己方的伤害就是技能增加的伤害,ΔAPS=原APS*持续时间/(CD时间-持续时间)。
软控:例如“沉默”(对方只能普攻不能用技能),先将其转化为硬控,与该属性等价的硬控的持续时间=软控的持续时间-软控的持续时间*对方普攻的APS/对方使用技能后的整体APS),然后再用硬控的公式。
施法时间:有施法时间的技能可能会被打断,因此不能稳定地提供 APS,可以设计一个基于施法时间的负向加成比例,ΔAPS=Δh/CD时间*(1+施法时间*加成比例),Δh是该技能所提高的伤害。
施法距离:站得越远越不容易受干扰,有效输出时间越长,可以设计一个基于距离的加成比例,ΔAPS=(Δh/CD时间)*(1+距离*加成比例)。
元素附着:因为后续可能会引发元素反应,可以设置一个加成比例,ΔAPS=Δh*(1+加成比例)/CD时间。
闪现:先拍脑袋定加成比例,ΔAPS=原APS*加成比例,后续测试的时候再观察带闪现的组的APS比不带闪现的组高多少。或者将闪现和一定量的攻击力作为对照进行测试,如果两个组战斗表现差异很大,就调整攻击力的量重新测试,最终将闪现对标到一个合理的攻击力区间。
…
将无法纳入伤害公式的防血类技能属性转化为EHP:
硬控/软控:控制类属性不仅可以当做攻击类技能属性转化为APS,也可以当做防御类技能属性转化为EHP。以硬控为例,能够减免的伤害比例=减免的伤害/总伤害=对方的APS*持续时间/对方的APS*CD时间=持续时间/CD时间,ΔEHP=原EHP/(1-持续时间/CD时间)-原EHP=原EHP*持续时间/(CD时间-持续时间)。
治疗:以一次性治疗为例,ΔEHP=治疗量*(生存时长/CD时间)。
…
在把技能属性转化为APS或EHP后,即可通过战力公式计算角色战力。计算战力的公式五花八门,这里列举两种最常见的:
公式一:战力=∑属性i的数值*属性i的价值。
属性价值可以理解为该战斗属性对角色战力的贡献大小,对于属性价值的确定,不同的书有不同的方法,这里演示其中一种。设生命值的属性价值为1,t表示生存时长,v表示攻击速度,dr表示免伤率,h表示一次攻击所造成的伤害,a表示攻击力,d表示防御力,x1...表示其他能够影响伤害的属性,则:
t=HP/DPS=HP/(v*h(a,d,x1...))→HP= t*v*h(a,d,x1...)→HP对影响h的各个属性求偏导,结果如下:
HP'(a)=t*v*h'(a):若攻方增加1点攻击力,守方必须同时增加t*v*h'(a)点生命值才能保证生存时长不变,故1点攻击力和t*v*h'(a)点生命值的价值相同,攻击力的属性价值为t*v*h'(a)。
HP'(d)=t*v*h'(d):若守方增加1点防御力,其必须同时减少|t*v*h'(d)|点生命值才能保证生存时长不变,故1点防御力和|t*v*h'(d)|点生命值的价值相同,防御力的属性价值为|t*v*h'(d)|。
…(HP对等其他属性求偏导,得出这些属性的属性价值)
t=HP/DPS=HP/(APS*(1-dr))→HP=t*APS*(1-dr)→HP对APS求偏导,结果如下:
HP'(APS)=t*(1-dr):1单位APS的价值为t*(1-dr),由此可以得出之前转化为APS的技能属性的价值,即ΔAPS*t*(1-dr)。(之前转化为EHP的技能属性的价值为ΔEHP*1)
从上面的演算示例中可以看到,属性价值并不是一成不变的,而是随着t、v等变量的变化而变化,如果用变化的属性价值来计算战力,则每次算战力之前都得先算一次属性价值,非常麻烦。而如果用固定的属性价值来计算战力,虽然计算很方便,但算出的战力却是不准确的,例如,代入毕业数值所求得的暴击率的属性价值是很高的,但前期由于玩家的攻击力很低,暴击率能提供的收益很小,用固定的属性价值去算前期的角色战力时,往往会导致算出的战力虚高。一个解决的办法是,根据集中投放属性的节点将养成划分为几个阶段,每个阶段求一次属性价值,从而减少一些误差。
除了属性价值会变化的问题,这一战力公式的结构也有问题,加法的结构使得即使攻和血中有一个为0,只要另一个够大,角色还能有不俗的战力,显然不合常理。
公式二:战力=EHP*APS。
设t表示生存时长, dr表示免伤率,则t=HP/DPS=EHP/APS,故:
比较A与B的战力 ⇔ 比较A与B的生存时长 ⇔ 比较A的EHP/B的APS与B的EHP/A的APS的大小 ⇔ 比较A的EHP*A的APS与B的EHP*B的APS的大小,故可以令战力=EHP*APS。
注:之所以不直接用t=HP/DPS,是因为DPS不仅与攻方的攻击类属性有关,还与守方的防御类属性相关,仅靠一方的属性求不出HP*DPS。
一般来说EHP*APS会是一个非常大的数值,不利于观察比较,可以定义一个相对战力来辅助理解,相对战力=战力/战力基准,战力基准取某个基准小怪的战力。相对战力为3表示在战斗中连续单挑3个基础怪物后会被杀死,假定一个首领怪的相对战力为5,两个相对战力为3的玩家组队即可通关。
与公式一相比,这一战力公式更自然也更准确,如果A的战力大于B的战力,则A的生存时长必然大于B的生存时长,相对战力的意义还要更加直观(详见上文)。此外,乘法的公式结构使得攻和血都不能太小,两类属性比较均衡时战力最大。
3.3 职业设计
参照1.2中给出的三个步骤:
STEP1明确求解对象:职业设计要给出的是每个职业的每个战斗属性相对于标准裸体人(不带任何武器装备的标准人)属性的换算系数,某职业某属性的投放量=标准裸体人该属性的投放量*相应的换算系数。
STEP2明确设计需求:职业设计的设计需求是保证各个职业战力平衡。
STEP3求解:基本思路是先根据每个职业的特点给出基础属性和技能属性,然后根据“该职业的战力=标准裸体人的战力”这一设计需求对给出的基础属性和技能属性进行整体放缩,得到最终的换算系数。
3.4 怪物设计
参照1.2中给出的三个步骤:
STEP1明确求解对象:怪物设计要给出的是每个怪物的每个属性相对于玩家属性的换算系数,某怪物某等级某属性的数值=对应等级下玩家的该属性数值*相应的换算系数。值得注意的是,怪物属性对标的是玩家属性而不是标准人的属性投放,因为大部分玩家并不能获取全部投放,玩家的属性数值=标准人的属性投放*预估的玩家平均获取比例。预估的玩家平均获取比例也可以估得细一点,即,分别估一下每个投放渠道玩家的获取比例,然后乘以该渠道的投放再汇总,这样后期验证和修正的时候也更方便。
注:由于玩家的属性数值是在不断成长的,一般会把怪物等级与角色等级对应起来,也可以对标游戏中的其他等级,只要这些等级能索引出玩家的属性数值即可,比如《魔兽世界》中怪物等级对标的是玩家的装备评分等级(一个战力指标),《原神》中怪物等级对标的是世界等级(世界等级的突破需要打通特定副本,故世界等级间接反映了玩家的战力水平)。
STEP2明确设计需求:怪物设计的设计需求是怪物生存时长和玩家生存时长之间的比例,这一比例的直观意义是“一个玩家能挑几个怪”。该比例可以用战力比来反映,因为在应用公式二的前提下,怪物生存时长/玩家生存时长=怪物的战力/玩家的战力,也可以用损血期望(玩家杀一个怪所损失的血量百分比)来反映,因为损血期望=怪的DPS*怪的生存时长/玩家的HP=怪物的生存时长/玩家的生存时长。
STEP3求解:基本思路是先根据每个怪物的特点给出基础属性和技能属性,然后根据对战力比/损血期望的设计要求对给出的基础属性和技能属性进行整体放缩,得到最终的换算系数。
3.5 战斗测试
战斗测试就是通过内部测试和公开测试验证设计需求的实现情况,并根据测试结果进行数值调优的过程。
内部测试一般有三种方法:VBA模拟,真实游戏模拟,AI大数据模拟。其中,VBA模拟适用于简单的战斗,是战斗模型要过的第一关;真实游戏模拟用贴近上线后真实情况的游戏原型做测试,是复杂战斗必不可少的验证环节;AI大数据模拟指用高智能AI模仿真实玩家进行大量战斗并生成海量参考数据,目前应用得很少。
公开测试主要指游戏的测试服测试,通过测试数据和玩家反馈验证设计需求的实现情况以及玩家对设计细节的接受程度,进一步优化数值模型。此外,游戏正式上线后的战斗数据和玩家反馈也可以看做一种公开测试,能够对之后版本的设计起到一定指导作用,少量情况下,还可对已上线的数值进行调强或暗中削弱。
调数需要大量经验积累,但VBA模拟却是可以快速学习的技能,因此这里主要讨论VBA模拟器的写法,基本步骤如下:
STEP1:定义玩家类,技能类,实例化玩家数组和技能数组,声明其他要用到的公共变量。
STEP2:编写主过程,内部顺序为初始化→{CD计算→技能检测→伤害计算→死亡判断},大括号表示循环,如果死亡则用End结束程序。每100ms进行一次循环就行,因为人的平均反应时间在300ms,极限反应时间也不低于100ms。
STEP3:编写初始化模块,要实现的功能是数据载入→清除之前的战斗日志→清除技能CD→显示hp和mp等信息。
STEP4:编写CD计算模块,循环所有技能,当冷却时间为0时不作处理,当冷却时间大于0时减少100ms的冷却时间。如果有公共CD还要再循环一遍公共CD。
STEP5:编写技能检测模块,循环所有角色,针对每个角色循环其所有技能,如果技能冷却时间为0且当前mp大于技能所需mp,则给攻方、守方、攻击技能这几个公共变量赋值→重置技能CD和公共CD→进入伤害计算模块→跳出当前的技能循环(对于同一个玩家,一回合只能出一个技能)。
STEP6:编写伤害计算模块,基本流程是判断命中/暴击(逐层法/圆桌法)→计算伤害/治疗→输出战斗日志(某某时间,某某的某技能对某某造成多少点伤害)→计算新的mp和hp,若计算结果小于0则令hp为0→显示新的mp和hp,如果守方死亡则在日志中输出死亡时间和死亡者。其中像“判断命中/暴击”和“计算伤害/治疗”这种比较复杂的步骤也可以单独封装为函数。
在伤害计算模块中,计算伤害之前要先判断本次攻击的概率判定情况(命中/格挡/暴击等),一般来说有两种判定方法——逐层法和圆桌法。假设伤害流程中共有三个需要判定的概率:命中率70%→格挡率8%→暴击率10%,则两种判定方法的判定过程如下:
逐层法:实际发生未命中的概率=1-70%=30%,实际发生格挡的概率=70%*8%=5.6%,实际发生暴击的概率=70%*(1-8%)*10%=6.44%,实际发生普通攻击的概率=100%-30%-5.6%-6.44%=70%*(1-8%)*(1-10%)=57.96%。优先极高的判定获益更高,处于低优先级的判定在计算其实际概率时,总要乘上若干个(1-n%)的因子,使之低于原始概率数字。优先级越低,这种衰减就越严重。
圆桌法:实际发生未命中的概率=1-70%=30%,实际发生格挡的概率=8%,实际发生暴击的概率=10%,实际发生普通攻击的概率=100%-30%-8%-10%=52%。如果未命中率和格挡率各自提高1%,暴击率还是10%,普通攻击减少为50%,所有除普通攻击外的判定概率在普通攻击被挤出圆桌前都是不会相互影响的。如果各自提高30%,普通攻击被挤出圆桌,暴击率就会减少为2%,在圆桌计算中优先级仍然存在,优先级低的判定会被率先挤出圆桌。
圆桌计算适合严格控制投放的模型,对概率值的变化很敏感,长期投放更适合用逐层计算,低优先级的属性可以投放很高的百分比数值,优先级越低,投放的值域范围就越大。
4 RPG数值——经济
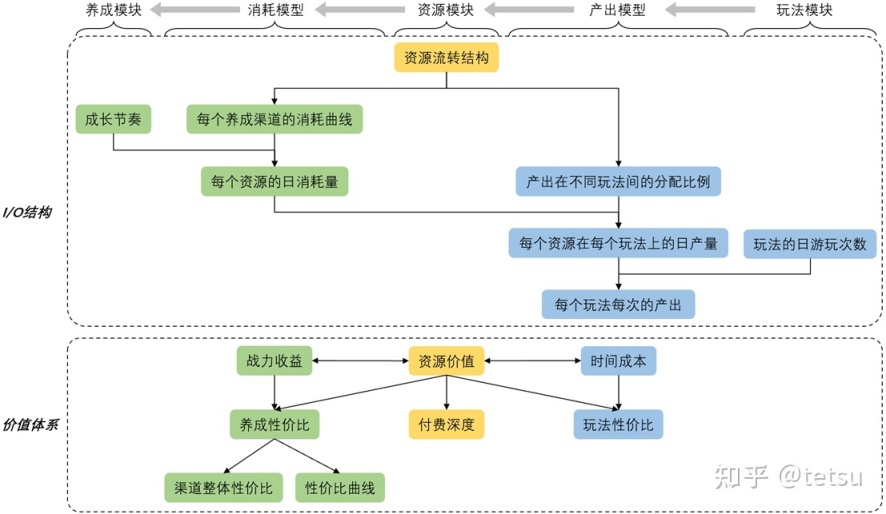
所谓经济就是资源管理,在RPG游戏中,资源由玩法模块产出再由养成模块消耗,形成了完整闭环的I/O结构。经济数值的设计目的就是规划好游戏中资源的消耗与产出,同时建立一套价值体系来衡量不同资源的价值。设计思路如下:
STEP1:确定资源流转结构。确定每个养成渠道消耗哪些资源、每个玩法模块产出哪些资源,画出资源流转结构图或黑点结构图。
STEP2:细化消耗模型的数值。确定每个养成渠道下每个被消耗资源的消耗曲线,结合2.1中规划好的成长节奏推出每个资源的日消耗量。
STEP3:细化产出模型的数值。确定每个资源的产出在不同玩法间的分配比例,结合第二步中得到的日消耗量推出每个资源在每个玩法上的日产量,再结合每个玩法每天的游玩次数推出每个玩法每次的具体产出数值。
STEP4:建立资源的价值体系。用资源价值作为桥梁把战力收益和时间成本联系起来,求出养成性价比、玩法性价比和潜在付费深度。
在做经济数值之前,还需要明确一下游戏的经济类型,常见经济类型如下:
计划经济:只允许玩家与系统交易,缺点是玩家之间的交互性差,游戏内的社区性会下降,适合偏单机的游戏,如《原神》。
市场经济:允许玩家之间自由交易,系统不参与。缺点是存在价格崩盘和游戏内容迅速消耗的风险,工作室、游戏商人等黑色产业也很容易滋生,对运营控制的要求极高,一旦崩盘玩家将快速流失,游戏寿命将大幅缩短。基本没有游戏是纯市场经济。
计划经济+市场经济:允许玩家间交易,但系统进行宏观调控。有一定交互性,风险也比市场经济小,适合绝大多数MMORPG,如《梦幻西游》。
如果是纯粹的计划经济,按照前述的设计思路建表即可。如果加入了市场经济,则还需要重点考虑以下两个设计难点:
盘活玩家交易:虽然游戏中会自然发生交易(例如,有时间没钱的玩家生产大量基础材料卖给有钱没时间的玩家,高等级玩家淘汰的装备道具卖给低等级玩家),策划仍可以通过复杂化生产端的方式进一步盘活交易,即,设计大量产出不同的玩法,玩家无法兼顾所有的玩法,自然会通过交易来获取资源,《梦幻西游》就是用的这种方式。
控制物价风险:控制物价最根本的是扩大消耗,因为随着运营时间的增长,产出会一直增加,消耗端不变的话一定会通胀,故需要持续不断地通过提高现有养成渠道等级上限或引入新养成渠道的方式制造新的消耗。设计养成渠道时需要让其容纳尽可能多的消耗,可以通过低概率极品的方式,比如《梦幻西游》的炼妖系统,《原神》的圣遗物系统,通过概率设计使得数值追求变得几乎无上限,养成深度大大加深。此外,为了缓解经济周期的波动、控制囤货炒作等操纵市场的行为,系统也需要对物价进行暴力干涉,手段有:限制个人每日的可交易游戏币上限、交易后物品需要冻结一段时间才能再次交易、交易价格区间限制、系统以设定好的价格参与买卖等。
4.1 资源流转结构
游戏中的资源可以分为养成类资源和玩法类资源,由于玩法类资源不在核心的I/O循环里,设计玩法系统时单独设计即可。这里主要讨论养成类资源。
资源流转结构是指游戏中资源流转的路径。设计时一般从养成模块逆推,先回答“每个养成渠道消耗哪些资源”,再回答“每个玩法模块产出哪些资源”,原因是设计游戏时一般会优先设计养成模块,且设计完成后基本不会再做调整。
资源流转结构有两种表示形式,一种是资源结构流转图,另外一种是黑点结构图。黑点结构图又可以分为消耗黑点结构图和产出黑点结构图。
以游戏《原神》为例,不考虑尘歌壶等相对比较边缘的系统,其资源结构流转图如下图所示:
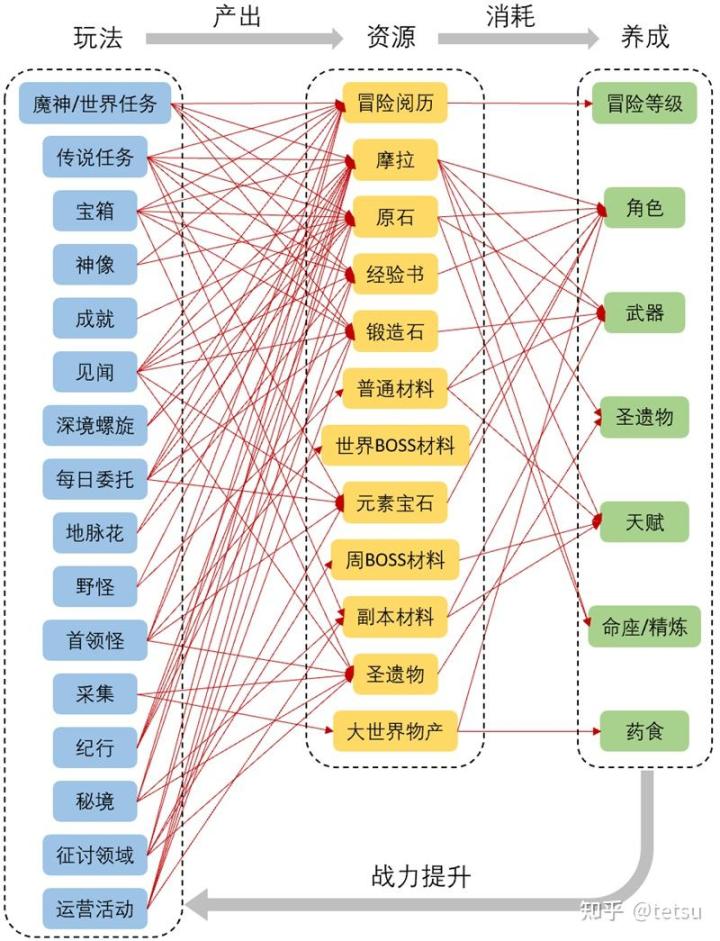
可以看到,资源流转结构图只适合比较简单的经济系统,遇到《原神》这样稍微复杂一点的系统后就会变得特别乱,因而更常用的其实是黑点结构图。《原神》的消耗黑点结构图如下图所示:

《原神》的产出黑点结构图如下图所示:
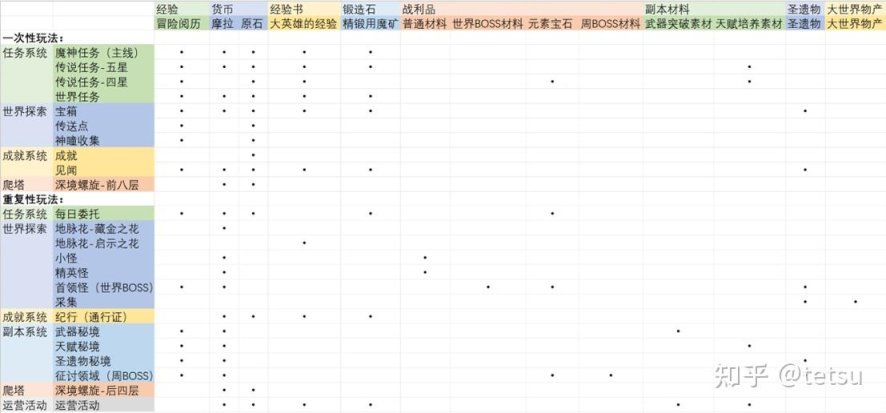
4.2 消耗模型
细化消耗模型一般分为两步,第一步确定每个养成渠道下每个被消耗资源的消耗曲线,第二步结合2.1中规划好的成长节奏推出每个资源的日消耗量。
注:由于横向收集型养成并不消耗资源,消耗模型只关乎纵向数值型或混合式的养成方式。
确定消耗曲线:
消耗曲线就是资源消耗量关于渠道等级的函数,一般来说每一级的消耗都是递增的,区别只在于递增的方式。加速递增比线性递增更为常见,前期用小额消耗制造高频反馈从而吸引玩家,后期用巨额消耗保证养成深度。
以《原神》为例,其各资源的消耗曲线如下图所示(笔者自己的粗略反推,不代表真实情况):

4.3 产出模型
细化产出模型一般分为两步,第一步确定每个资源的产出在不同玩法间的分配比例,第二步结合消耗模型中的日消耗量和每个玩法每天的游玩次数推出每个玩法每次的具体产出数值。
确定产出分配比例:
其实就是把产出黑点结构图中的黑点换成分配比例。给比例的时候要注意给那些核心的、耗时长的、可玩次数少的玩法分配更高的比例,否则会出现激励扭曲,即,玩家为了高奖励去玩一些不重要也不有趣的玩法,进而厌烦游戏。此外,要尽量使每个资源的产出都集中在少数玩法上,每个玩法的产出都以少数资源为重心,形成资源与玩法的强对应,从而降低玩家的理解成本,促使玩家更有针对性地去做某件事,目标更明确。
以《原神》为例,其产出分配比例大致如下图所示(笔者自己的粗略反推,不代表真实数据):
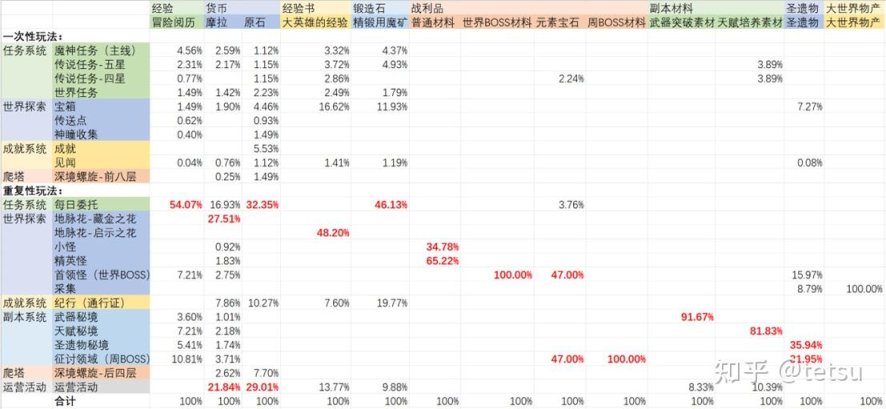
可以看到,《原神》中的每个资源都有1-2两个最主要的来源(红字部分),冒险阅历主要来自每日委托,摩拉主要来自藏金花和运营活动,原石主要来自每日委托和运营活动,经验书主要来自启示花,锻造石主要来自每日委托…比例框架中蕴涵着资源与玩法的强对应关系,降低了玩家的理解成本。值得注意的是,《原神》给每日委托和运营活动这两个非核心也不那么有趣的玩法分配了较高的产出比例,这可能会产生一定程度的激励扭曲,是其作为长线运营游戏,为保证月活与日活的无奈之举。
推出单次产出数值:
某玩法每次的A资源产出=A资源的平均日消耗量*A资源对该玩法的产出分配比例/该玩法每天的游玩次数。实际计算并没有这么简单,因为会有一些需要控制的设计需求,例如:
固定产出和随机产出的比例:如果事先设定了固定产出和随机产出的比例(这一比例对于不同的玩法可能不同),则某玩法每次的A资源固定产出= A资源的固定产出比例*A资源的平均日消耗量* A资源对该玩法的产出分配比例/该玩法每天的游玩次数。
可流通产出和不可流通产出的比例:如果事先设定了可流通产出和不可流通产出的比例(这一比例对于不同的玩法可能不同),某玩法每次的A资源可流通产出= A资源的可流通产出比例*A资源的平均日消耗量* A资源对该玩法的产出分配比例/该玩法每天的游玩次数。
针对不同程度付费玩家的投放比例:不同程度付费玩家的成长节奏是不一样的,因而资源的日消耗量和单次产出量也是不一样的,需要对免费玩家的单次产出量进行放大。
4.4 价值体系
所谓建立资源的价值体系就是确定游戏中各个资源的价值。把I/O模型当做一个整体来看,玩家付出的直接成本是时间,获得的最终收益是战力,玩家在玩法模块付出时间成本获取一定价值的资源,在养成模块付出一定价值的资源获得战力收益,资源作为连接时间成本和战力收益的桥梁,其价值的衡量显然有两个思路:
用战力收益衡量资源的价值(从养成模块向玩法模块逆推):假设每点战力的价值为n,资源A,资源B,资源C…的价值分别为a,b,c…。挑选部分养成渠道,令升级的成本与收益相等,可得方程组:某养成渠道升级所提高的战力*n=该养成渠道升级所需的A资源个数*a+该养成渠道升级所需的B资源个数*b+…,解多元方程组即可得到每个资源的价值。
用时间成本衡量资源的价值(从玩法模块向养成模块正推):假设每小时时间价值为m,资源A,资源B,资源C…的价值分别为a,b,c…。挑选部分玩法,令游玩的成本与收益相等,可得方程组:某玩法完成一次所花的时间*m=该玩法产出的A资源个数*a+该玩法产出的B资源个数*b+…,解多元方程组即可得到每个资源的价值。
注:实践中思路一用得更多,原因是设计游戏时一般会优先设计养成模块,且设计完成后基本不会再做调整。
建立资源的价值体系有两个最主要的用途,一是衡量不同养成渠道、不同玩法的性价比,二是预估游戏的付费深度。
计算性价比:
玩法性价比=该玩法产出的资源收益/该玩法耗费的时间成本,玩法性价比一般用于对比不同玩法的划算程度,不同玩法的性价比应当尽可能均衡,差异过大的话部分玩法将会变成鸡肋。此外,越核心越有趣的玩法,其性价比也应当越高,否则会出现激励扭曲,即,玩家为了高奖励去玩一些不重要也不有趣的玩法,进而厌烦游戏。
需要计算的养成性价比有两种,一是养成渠道整体的性价比,渠道整体性价比=该渠道获取的所有战力收益/该渠道消耗的所有资源成本,渠道整体性价比一般用于对比不同养成渠道的划算程度,不同养成渠道的性价比可以不用那么均衡,渠道间的性价比差异可以使游戏的养成模块整体呈现出边际收益递减的趋势,从而适配不同深度的玩家。二是性价比曲线,算出渠道内每一次升级的性价比并将其绘制成一条曲线,性价比曲线一般用于观察某个养成渠道内部的性价比趋势,根据2.2的讨论,属性成长一般都是线性的,即每一级增加的战力是相等的,而根据4.2的讨论,每一级消耗的资源却是递增的,故性价比曲线大都呈现波动递减的趋势,这能够在游戏初期给到玩家最大的收益刺激,从而吸引更多的玩家。
注:在确定资源价值时如果采用了思路一,则对于那些被挑选的养成渠道,其性价比一定为1,其他养成渠道的性价比会在1附近波动,玩法性价比的量级取决于n的大小,为了方便观察,最好通过取合适的n让玩法性价比也在1附近波动。如果采用了思路二,则对于那些被挑选的玩法,其性价比一定为1,别的玩法的性价比会在1附近波动。养成性价比的量级取决于m的大小,为了方便观察,最好通过取合适的m让养成性价比也在1附近波动。
预估付费深度:
游戏付费可以分为养成模块付费(购买养成资源)和玩法模块付费(购买玩法资源)。RPG游戏大都以养成模块付费为主,付费深度=∑养成渠道i所消耗的全部资源的价值*养成渠道i预设的付费比例。
更多游戏资讯请关注:电玩帮游戏资讯专区
电玩帮图文攻略 www.vgover.com

















