概率補償——爲了遊戲體驗的巧妙設計

Intro——完全隨機的遊戲belike

讓我們構想一個情景：你正在玩一款類Dota遊戲，渡劫局，贏了這把就能升到最高段位。

這局遊戲中你是遠程大哥位，依仗暴擊的那種射手。經過線上的唯唯諾諾，矇頭苦刷，你通過裝備將自己的暴擊率提升到50%。

接下來是重要的資源團戰，你精緻走位，瘋狂平A，但是你逐漸發現不對，明明有50%的暴擊率，但是你就是A不出幾下暴擊，只能看着對面的戰士瘋狂打亂你們的團戰陣型。然後你輸掉團戰，節奏一塌糊塗，輸掉對局，渡劫失敗，被隊友沒收雙親，你憤而刪遊。

結束。

這就是沒有概率補償的類Dota遊戲中極大可能出現的情況，在某些關鍵的節點，隨機性並沒有那麼可靠，因爲隨機性真的太過隨機了。

面板數據隨機性的數學解讀

一枚完全質地均勻，六面質量相同的理想骰子，投擲一次得到每一面的幾率都是1/6，數學上稱之爲古典概型。試驗中所有可能出現的基本事件只有有限個，且試驗中每個基本事件出現的可能性相等。

那麼假設玩家此時暴擊率爲50%，作爲古典概型是否適合在遊戲中表達呢？

還是回到骰子，此時骰子就在你的手上，連續投出六次，奇了怪了，居然全是六點。你又投了六次，這次居然又全是三點。你感到疑惑。

不是說好的1/6嗎？

那麼這裏就要提到樣本容量。樣本容量是指一個樣本中所包含的單位數，你一共投了六次骰子，那麼樣本容量爲六次。樣本容量的大小與推斷估計的準確性有着直接的聯繫，在總體既定的情況下，樣本容量越大其統計估計量的代表性誤差就越小，反之,樣本容量越小其估計誤差也就越大。

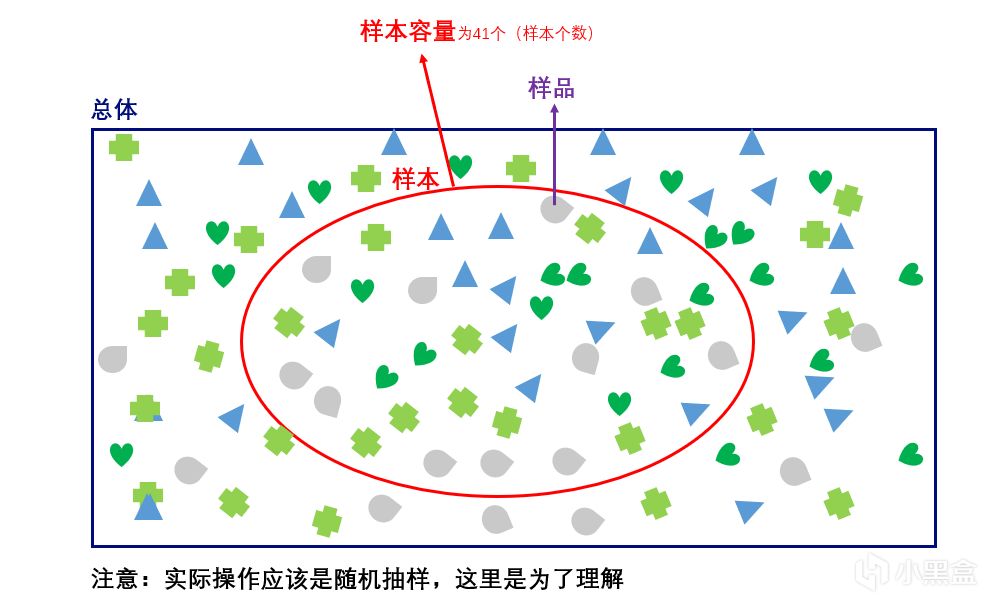
圖源：https://www.cnblogs.com/yanFlyBlog/articles/14752635.html

六次是一個很小的樣本容量，所以你有很大的可能並不能得到1/6這個值。而當你連續投上一萬次，十萬次，更多次，那麼最終得到的數據將無限逼近1/6。

回到遊戲上，人們對於概率的第一感知是片面的，因爲樣本容量難以直觀感受。人們會自然地將視線關注到極端現象以及關鍵數據：比如連續沒有達成其中某一結果，或者關鍵團戰的概率結果。

舉個例子，假設你保持50%的暴擊率，在整局遊戲中平A了一萬次，最後統計，從總體來看，你暴擊的次數在五千次左右，沒有問題。可是你就是在關鍵團戰中，一次暴擊也沒A出來。就這樣，一段“合理“的極端情況毀掉了你一整局的遊戲體驗。

那有沒有辦法避免這樣的極端情況，同時儘可能保持暴擊率呢？

遊戲設計師：“有的兄弟，有的！”

☝️🤓

概率補償——爲了遊戲體驗的巧妙設計

《魔獸爭霸3》的設計師給出了“概率補償”這一天才設計：

還是面板50%的暴擊，這次我們這樣設定——實際上，你第一次的暴擊幾率並沒有50%，而是25.7%，如果這一次攻擊沒有暴擊，那麼下一次攻擊的暴擊幾率提升到51.4%，以此類推，在第四次攻擊時提升至100%。當產生暴擊，下一次攻擊的暴擊幾率再次回到25.7%。

我們來簡單通過馬爾可夫鏈的穩態概率計算一下，按照這樣設計的實際暴擊率是多少？

狀態0：初始狀態，暴擊概率爲25.7%（0.257）。

狀態1：前一次未暴擊，當前暴擊概率爲51.4%（0.514）。

狀態2：前兩次未暴擊，當前暴擊概率爲77.1%（0.771）。

狀態3：前三次未暴擊，第四次必定暴擊（100%）。

狀態0：暴擊後仍爲狀態0（概率0.257），未暴擊轉移到狀態1（概率0.743）。

狀態1：暴擊返回狀態0（概率0.514），未暴擊轉移到狀態2（概率0.486）。

狀態2：暴擊返回狀態0（概率0.771），未暴擊轉移到狀態3（概率0.229）。

狀態3：必定暴擊，返回狀態0（概率1）。

設穩態概率爲π₀（狀態0）、π₁（狀態1）、π₂（狀態2）、π₃（狀態3），滿足：

π₀ = 0.257π₀ + 0.514π₁ + 0.771π₂ + π₃ 

π₁ = 0.743π₀ 

π₂ = 0.486π₁ 

π₃ = 0.229π₂ 

π₀ + π₁ + π₂ + π₃ = 1

得到：

π₀ ≈ 0.4572, π₁ ≈ 0.3397,  π₂ ≈ 0.1651, π₃ ≈ 0.0378

平均暴擊率爲各狀態暴擊概率的加權和：

{平均暴擊率} = 0.257π₀ + 0.514π₁ + 0.771π₂ + 1.0π₃ ≈ 45.74%

按照該機制，實際平均暴擊率約爲 45.7%。

概率補償的數學表達

與面板上的暴擊率存在一定的差距，但是通過概率補償，我們可以明顯看到它避免了極端數據的出現：降低第一次暴擊的概率，一定情況下避免了“刀刀烈火”的出現（所以S8的JackeyLove向前閃現的四下暴擊真是難得）；而同時增大後面攻擊的暴擊概率，避免了死活打不出暴擊的情況。

儘管實際的暴擊率低於面板上的，但是你的遊戲體驗得到了保障。

“嘰裏咕嚕說啥呢，我玩百爆的😋😋”

概率補償的應用不止於遊戲中的數值計算：抽卡，裝備強化，掉落機制等等機制中都能見其身影。

同時針對不同機制需求，概率補償得具體形式也有不同側重的分化：遞增型概率補償（剛纔已經提過），保底機制（Hard Pity，設置絕對上限，失敗次數達到閾值後強制成功），衰減型補償（反向調控，連續成功後降低概率，防止過度收益），動態平滑算法（如PRD僞隨機，通過數學公式（如馬爾可夫鏈）動態調整概率，使結果分佈更接近“人類直覺”），有機會我們再單獨討論。

從體驗上來說，玩家對“公平性”的感知比數學真實更重要（至理），人的感知有限，10%暴擊率若連續10次未暴擊，會被認爲“虛假”。“概率補償”通過巧妙的算法，實現了一定程度的“數學真實”與“玩家體驗”的平衡。讓隨機性更好地服務於遊戲。