張益唐——黎曼猜想，華人數學家再創重大突破！

11月5日，華人科學家張益唐教授，在山東大學分享了他最新的學術成果，論文主題爲朗道-西格爾零點猜想，該猜想主要解決廣義黎曼猜想中L函數是否存在異常零點的問題，張益唐本人相當自信，預計論文在同行評審通過後，將成爲數學史上又一里程碑的突破，而且會比張益唐在孿生素數猜想上的成就意義更大！

七大難題

黎曼猜想，是波恩哈德·黎曼在1859年提出的，接近200年的時間裏，黎曼猜想成爲數學家最感興趣，同時也是數學界最重要的問題！在千禧年之際，麻省劍橋市的克雷數學研究所，選出了七個“世界難題”，每個問題都象徵性地懸賞一百萬美元。

“七大難題”包含NP完全問題、龐加萊猜想、楊-米爾斯存在性和質量間隙等難題，黎曼猜想正是其中之一。在此之前，普遍科學家認爲廣義黎曼假設預計是正確的；截至目前，已經有上千條數學命題是以黎曼猜想的證明作爲前提存在的，那麼黎曼猜想與本次張益唐教授的成果有何關係呢？

朗道-西格爾零點猜想（Landau-Siegel Zeros Conjecture），是黎曼猜想的某種弱形式，通常也被視作黎曼猜想的核心問題，如果論證這個所謂的朗道-西格爾零點不存在，那麼上千個數學命題將直接晉升爲公理；若零點存在，那麼將與黎曼猜想產生衝突......

素數

1859年8月，32歲的數學家黎曼，向柏林科學院提交了一篇論文，題目爲“論小於一個給定值的素數的個數”，短短八頁的論文中的猜想成爲後世數學家奮力解決的問題，文中黎曼所探究的問題其實相當相當簡單，只需要小學三年級學生就能看懂，黎曼拋出問題：小於20的素數有多少個？

答案是8個：2，3,5,7,11,13,17和19。黎曼繼續發問，小於1000的素數有多少個？小於100萬呢？小於10億呢？儘管我們今天的超級計算機輕鬆給出答案，小於1000的有168個素數，小於100萬有78498個，小於10億的有50847534個，數學家高斯則親手統計過300萬以內的素數，但我們依然需要一個普遍的規律或公式，來確定素數的分佈情況。

黎曼提出了對這個問題的一個猜想，然後附文寫道，“人們當然希望對此有一個嚴格的證明，但是我稍稍做了一些徒勞的嘗試後，便把尋求這樣一個證明的事擱置一邊，因爲它對於我目前的研究工作並不是必需的”，恰恰是這個不算太起眼的猜測，成爲數學界最重要的謎題，這個猜測日後被稱爲“黎曼假設”/“黎曼猜想”。

素數定理

討論素數，我們很容易發現自然數越靠後的數字，素數出現的頻率似乎越低，經過簡單統計，1到100之間有25個質數；401到500之間有17個；901到1000只有14個；像這樣每隔100個整數取一次，一直列到10000億，最後一組百數段裏僅有4個素數。如果這樣一直到萬億萬億萬億萬億，最後在某一個地方之後素數會不存在嗎？

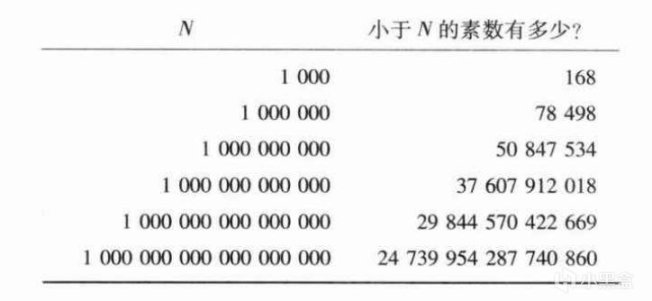
這個問題早在公元前300年，歐幾里得就已經給出了相當完備的證明，他認爲素數永遠不會稀疏到沒有，即沒有最大的素數——素數無限定理，歐幾里得假設從p1開始一直到pn均爲素數，最大的素數爲pn，構造一個s = (p1 x p2 x p3 x ... x pn) + 1 的數，若s爲素數，那麼s>pn與假設矛盾，若s並非素數，那麼s不能被已知最大的素數整除，同樣矛盾。

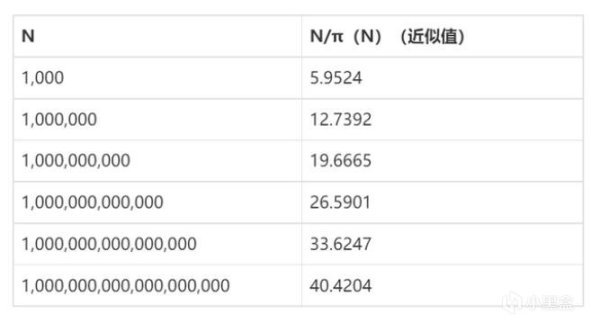
已知素數有無窮多個，再來考慮素數的分佈問題，上面我們用π(N)來表示“小於（等於）N的素數個數”，再簡單用N/π(N)，得到了一組似乎是以7爲公差的等差數列，這僅僅是巧合嗎？我們再將對數log N對比列出來，可以發現，當N越大的時候，N/π(N)越接近log N。

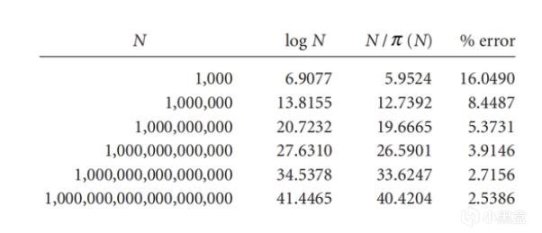
黎曼ζ函數

有了這一發現後，我們按照歐拉使用的數學符號得到上面的素數定理，接下來的內容則涉及到高數/數分，我們從調和級數開始入手，調和級數可以簡單理解爲調和數列（各項倒數爲等差數列的級數）各元素之和，可以通過Cauchy判別法判斷，所有調和級數都是發散的（Divergent）。

原本的調和級數如下式，即1,2,3,....各項倒數所成的數列，我們繼續推廣，1,2,3,....平方的倒數所組成的數列，即級數1+1/4+1/9+1/16+...，歐拉給出了極限爲π^2/6，即自然數平方倒數之和等於π^2/6，每一個初次看到這個證明的人都會爲數學的神奇震驚不已，我們繼續推而廣之。

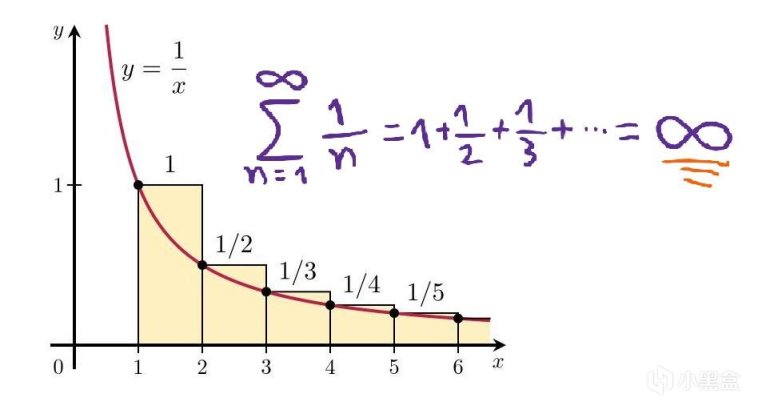
將調和級數推廣到下面的ζ函數（Zeta Func），上面自然數平方倒數之和可以理解爲ζ(2)，上面第一段的調和級數ζ(1)→∞，歐拉繼續證明ζ(2)=π^2/6，最終在1737年發現歐拉乘積公式，初步探究到ζ函數與素數存在某種關係，黎曼進一步思考，如果ζ函數里的s均爲素數呢？

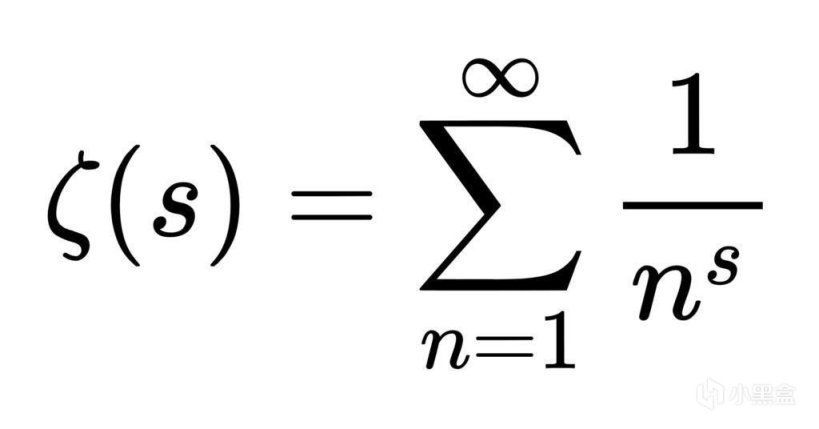
黎曼猜想

黎曼研究的領域極廣，同時也是複分析的創始人之一，他發現如果從複平面上思考Zeta函數，會出現很有意思的變化。複平面上X軸對應實部，Y軸對應虛部，將複數輸入ζ函數，發現僅有在實部大於1的情況下級數才收斂。原有的ζ函數只滿足實部 Re(s) > 1的情況，黎曼於是進行了“解析延拓”。

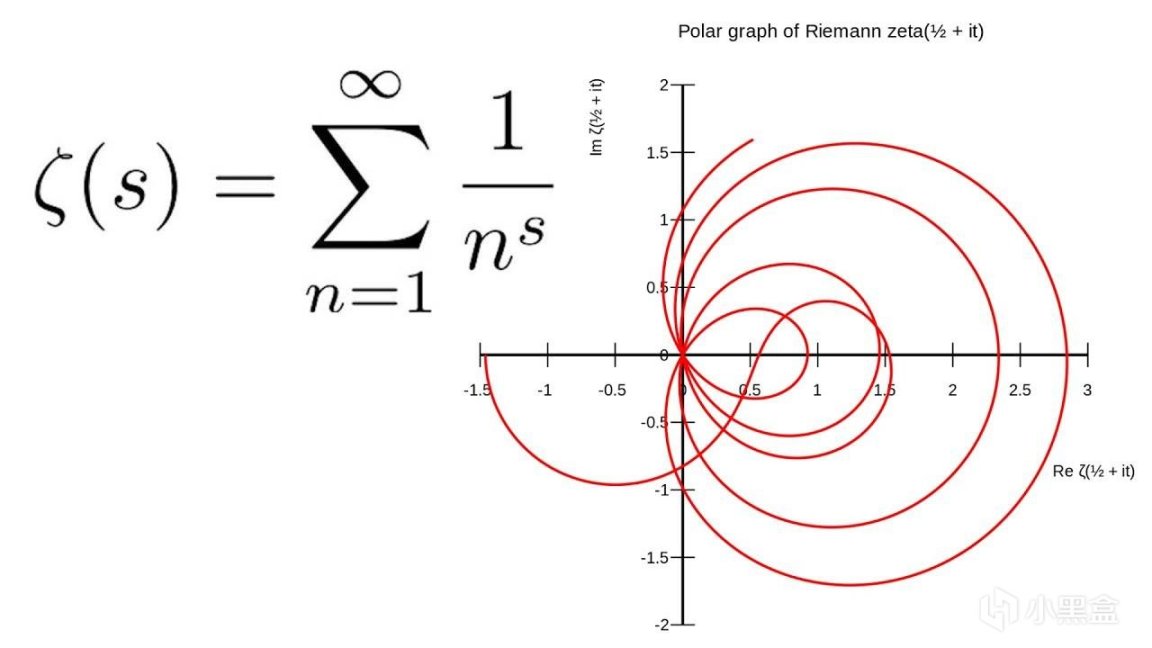
這部分的可視化可以參考3B1B的視頻，黎曼對歐拉的ζ函數進一步推廣到複平面，即填補Re(s) < 1的函數，使得黎曼ζ函數同時符合歐拉常規的s與複平面上的s，下圖中左半部分即爲解析延拓的可視化，它們不是被求和算出來的，而是通過解析延拓證明出來，且具有唯一性，當s=-1時，我們可以得出ζ(-1)=-1/12（注：該式非自然數和）。

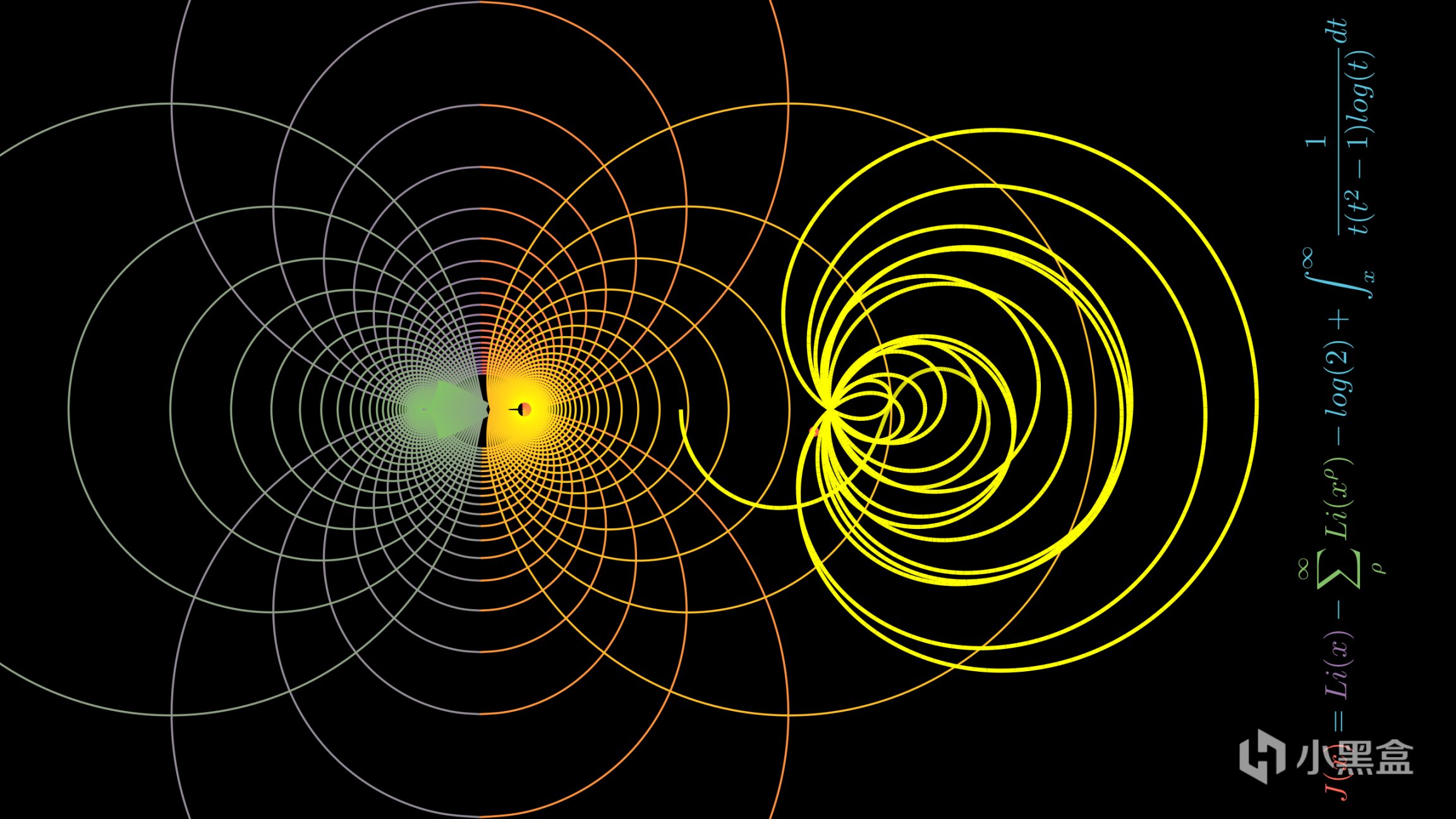
有了以上基礎，我們推導出黎曼ζ函數滿足以下代數關係式，我們發現當S=-2n時ζ爲零，我們將其稱爲黎曼ζ 函數的零點，這一部分零點分佈有序，我們將其稱爲平凡零點 (trivial zero)，其他零點則稱爲非平凡零點，黎曼給出猜想是，黎曼ζ函數的所有非平凡零點，都位於複平面上 Re(s)=1/2 的直線上，即實部=1/2的軸上，換句話說，方程ζ(s)=0的解的實部都是1/2。

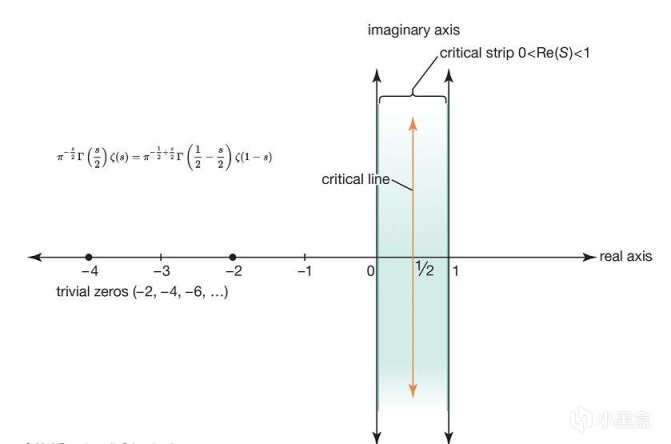
朗道-西格爾零點猜想

黎曼猜測Zeta函數所有非平凡零點都在實部1/2的直線上，此後多位數學家在黎曼ζ 函數的基礎上不斷打“補丁”，到了十九世紀，數學家狄利克雷引入L函數，相信很多人都聽說過狄利克雷定理，即對於任意互質的正整數a,d，有無限多個形式如a+nd的素數。

於是描述狄利克雷L函數的黎曼猜想被稱作廣義黎曼猜想（GRH），原問題從黎曼ζ 函數非平凡零點都在實部1/2的直線，變成L函數的非平凡零點都位於1/2直線上，西格爾給出ξ函數數值的計算方法，他與老師朗道一起發現了L函數理論中的零點現象，並且確定非平凡零點基本上落在類沙漏的區域，此前Atiyah爵士曾自稱證明了黎曼猜想，而張益唐在07年曾給出過L函數非平凡零點的下界估計。

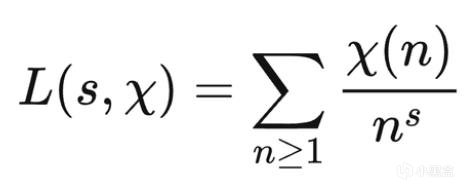
但當時的理論還存在瑕疵，於是張益唐13年在孿生素數方向取得突破性研究，確立了存在無窮多差小於7000萬的素數對，有了這一基礎，22年的菲獎得主詹姆斯·梅納德對孿生素數繼續進行優化；今天張益唐的新論文也是拋出了L函數在1處的下界(log D)^(-2022)，這裏-2022也相當具有代表意義，如果方法成行，那麼有機會像孿生素數那樣繼續優化，直到L函數要求的-1。