什麼是邏輯解謎?這個詞並沒有一種大家都承認的定義,但我個人將其定義爲“基於一套可以用嚴謹的數學語言表述的底層規則/邏輯的解謎”,不管這套規則實際上表述起來有多複雜。比如大家耳熟能詳的《推箱子》就可以用“有限狀態機”這樣的東西給出一套嚴謹的定義,但我在這裏就不定義給大家看了。而至於《鏽湖》這樣的指向點擊解謎,雖然可能內含單個的邏輯謎題,但大多數不屬於我所定義的“邏輯解謎”。
對於這類遊戲,我不止一次聽到這樣的聲音:“這種遊戲就和做題一樣,沒什麼意思”。這我並不完全否認,但肯定也不完全同意。“像做題”這個表述比較籠統,到底是在哪方面“像”呢?是說邏輯解謎和做題一樣重複和枯燥無味嗎?還是說邏輯解謎和做題一樣,一旦不會就只能看答案,只是因爲沒有出題人一般的超強“注意力”?
我不知道屏幕前的你有沒有看過“3Blue1Brown”這位知名數理科普博主的視頻,我也不止一次看到有評論說這個頻道“重新點燃了其對數學的熱情”。舉這個例子是想表明,我認爲並不是“數學”或者“數學題”本身枯燥,有可能我們只是沒有掌握正確的思維方法,對於邏輯解謎當然也是一樣。
所以這篇文章的目的就此顯現:我希望通過分享我個人遊玩邏輯解謎的經驗,包括我的解謎思路和“技巧”,來讓大家感受到邏輯解謎遊戲中蘊含的邏輯之美。

遊戲:Jonathan Blow開發中的推箱子新作
(有些插圖只是爲了讓文章看上去沒那麼“幹”,當圖片真的和文字有關的時候我會說的)
我不太清楚屏幕前的各位之前是怎麼“解謎”的,我覺得無論你熟不熟悉解謎遊戲,也不管你能不能將你自己的思路明確表達出來,只要你嘗試過解謎,在你大腦中一定有某個部分負責這個過程當中的邏輯思維,儘管你可能覺得這只是某種“直覺”,或者是某種專屬於所謂“大佬”的“注意力”。
而且,幾乎所有的解謎遊戲攻略只包含實際上“輸入”解謎步驟的過程,而不包含解謎背後的思維方法,這就更會加深玩家對深度解謎玩家的“刻板印象”,認爲“他們就是比我聰明”或者“他們就是注意力比我強”。
解謎遊戲不是搞學術,因此不需要“防禦性證明”(只能看出來是對的,但完全看不出來是怎麼想出來的)。我在這裏想做的,就是嘗試把這些背後的“直覺”明確地表述出來,從而給大家展示我自己解謎時,遇到靠直覺無法解決的謎題時(也就是大部分時候),我能從什麼角度去思考問題。
下面,我會先列舉一些在我看來有用的解謎策略,然後用一些具體謎題的例子手把手帶大家領略我自己的解謎思路。
策略一:試錯
這可能是大部分玩家碰到無法立刻通過的謎題時的第一反應,畢竟如果胡亂試一試就能通過的話,爲什麼要動腦呢?雖然很簡單粗暴,但又不得不承認,在某些情況下,試錯確實就是最有效率的做法。
具體來說,這種策略就像是在走迷宮:
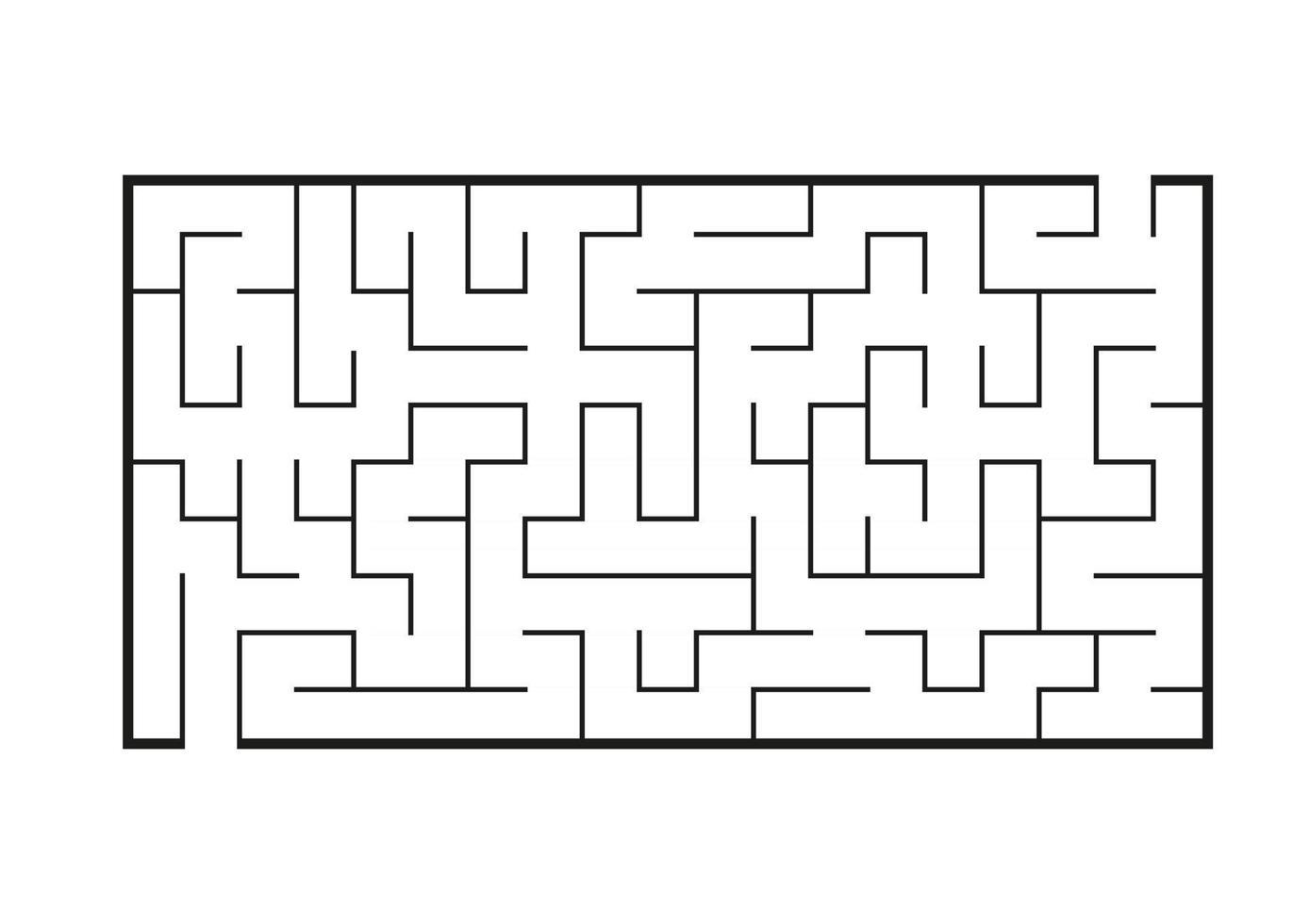
從起點出發,找到一條符合直覺的路往下走,如果走不通,就倒回去,在最後一個岔路選擇另一條路走,一直走到終點爲止。而在大多數的邏輯解謎遊戲中,關卡狀態的變化實際上就形成了“隱式”的迷宮,那麼當然也就可以使用類似的策略。
然而,試錯策略仍然具有下列問題:
絕大多數邏輯解謎的“狀態迷宮”都不如上面圖片中的迷宮這麼容易理解,不太可能“縱覽全局”。在邏輯解謎遊戲中,試錯的體驗其實更接近“第一人稱走迷宮”,手上沒有地圖的那種。
考慮到上面這一點,有時要記住自己探索過哪些方向也是非常困難的。我到底有沒有走過這條路?有沒有到過這個岔路口?有時,我們甚至很難看出一個局面下的所有可行選擇,更別說枚舉了。稍有不慎就可能有重複或遺漏,導致你在狀態迷宮中“迷路”。
如果一個謎題看上去有太多的可能性,完全不能枚舉,那麼試錯策略明顯就不管用了。就算能用,很多時候通過試錯來解謎也並不會產生核心的“尤里卡”時刻,因爲這和模擬計算機搜索沒什麼區別,沒有什麼獨屬於人類的“邏輯美感”。
那這個時候怎麼辦呢?放棄嗎?當然不是。我們首先想一想,“試錯”的本質是什麼?是通過親自探索來確認每條“路”是能走通還是走不通。那如果我們有辦法,不用親自把每一條岔路都走完,就知道它們能不能走通呢?
恭喜你,你剛剛發現了“剪枝”的思想,而接下來要說到的所有策略,本質上都是通過人類邏輯做到了剪枝。
策略二:尋找瓶頸步驟
我覺得說這是我個人在解謎中用到的最重要的策略也不爲過。它是很多種小策略的集合,但是目標一致,所以就直接合起來說了。
瓶頸步驟就是在解決一個謎題過程中必須要經過的步驟。繼續以“迷宮”爲例:
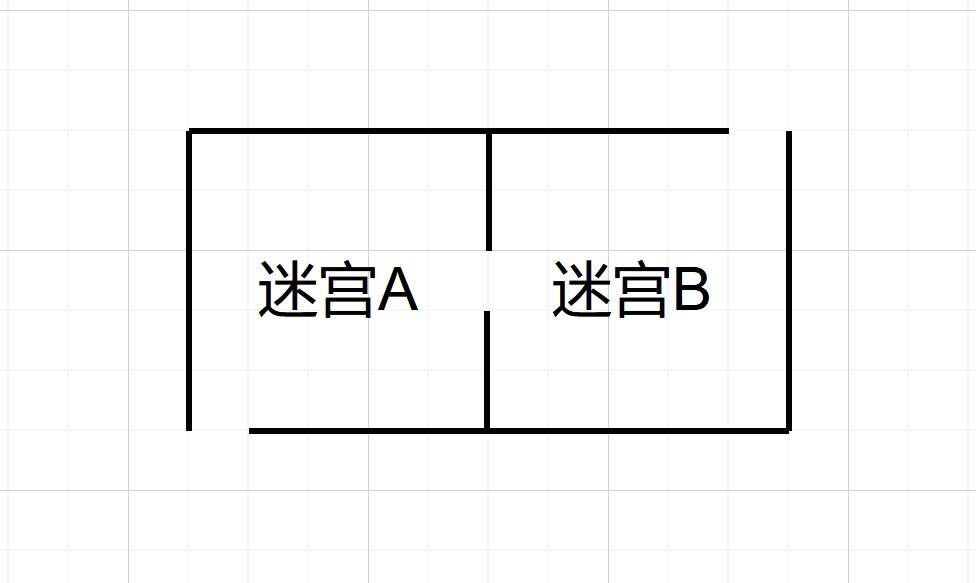
假設有這麼一個迷宮,你需要從左下角到達右上角,而迷宮中間有一條明顯的分界線,且分界線中間只有一個開口。在考慮正常解法(即不能從外面走,不能穿牆,等等)的前提下,你能夠獲得什麼結論?沒錯,那就是路線必須要經過中間那個開口。
那這又有什麼幫助呢?可以看出,整個迷宮現在就被分界線分成了“迷宮A”和“迷宮B”兩個部分,現在你只需要分開解決兩個迷宮就可以解開整個迷宮了。
是的,找到瓶頸步驟最大的作用,就是將謎題這個“大問題”分成更多更容易的“小問題”,這也就是經典的“分治”思想。
比如對於上面的第一個迷宮,我們就可以找到下面標紅的“分界線”:
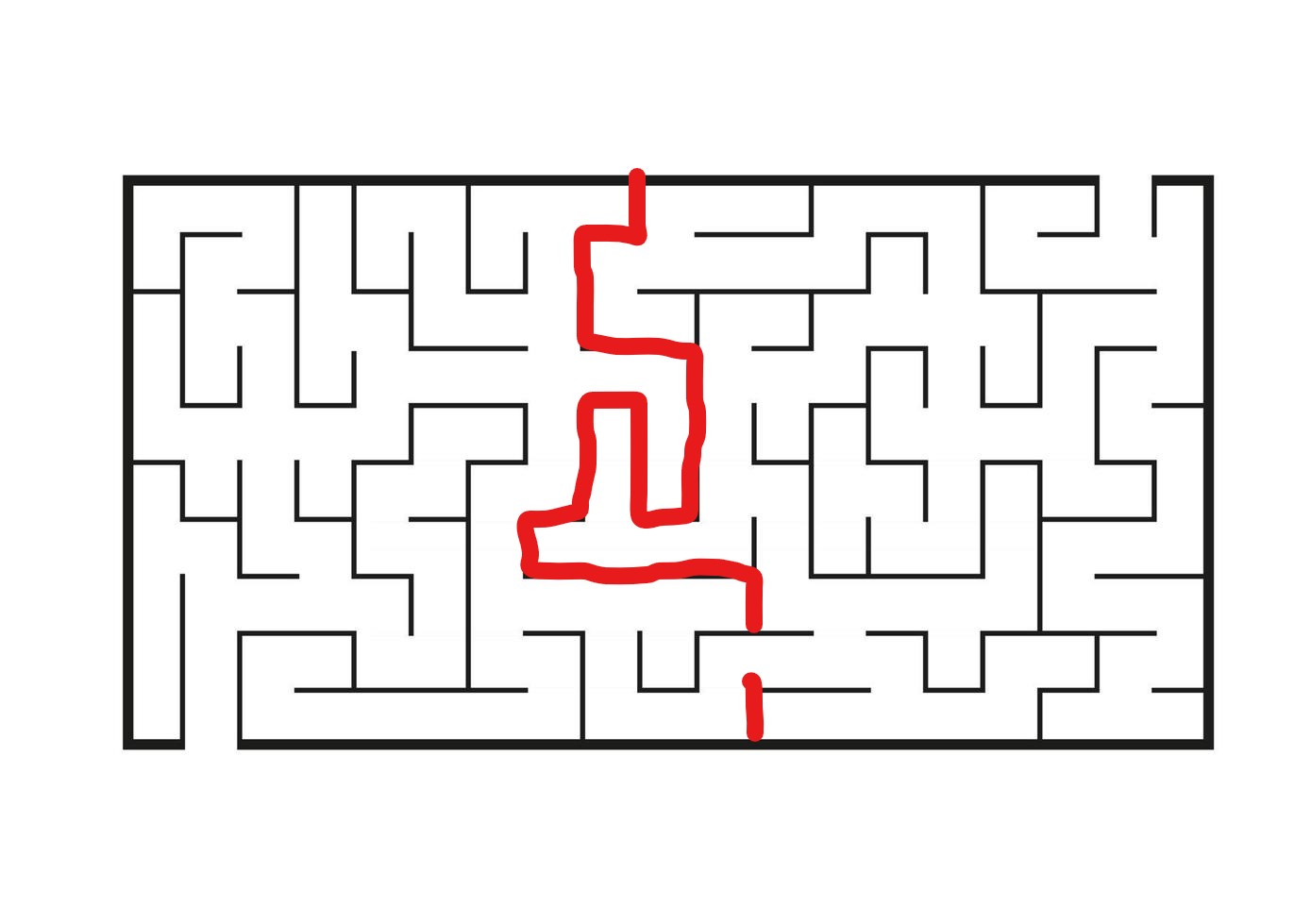
當然這只是舉個簡單的例子,如果你可以用其它更簡單的方式解開謎題,那自然沒有必要用到更復雜的策略。只不過,在實際應用中,很多時候你面對的問題都並不像這個迷宮這麼簡單,此時找到一些關鍵的瓶頸步驟就能大大減少試錯的量。
要尋找一個謎題的瓶頸步驟,也有很多種方法。你可以直接問自己:“如果要解決這個謎題,有哪些事情是必須要發生的?”,然後從那些事情開始想,注意結合其它的策略。
如果你還是覺得困惑,不妨從一個謎題必須要到達的狀態開始想:目標/終點。沒錯,從終點開始倒推也是一種非常常見的解謎思路,且很多時候比正着推要更有頭緒。
策略三:證明高級結論
請不要一看到這麼“數學化”的表達就被嚇到,我只是實在不知道怎麼用最少的詞語概括這種思維方式了。
在邏輯解謎遊戲中,有時我們會得到比“在這個狀態下,這麼移動,就能到達另一個狀態”更高一級的結論,這些結論通常會爲我們對謎題中“什麼必須發生”和“什麼必須不能發生”提供幫助。
在這方面,我能想到的最簡單的例子就是《推箱子》:
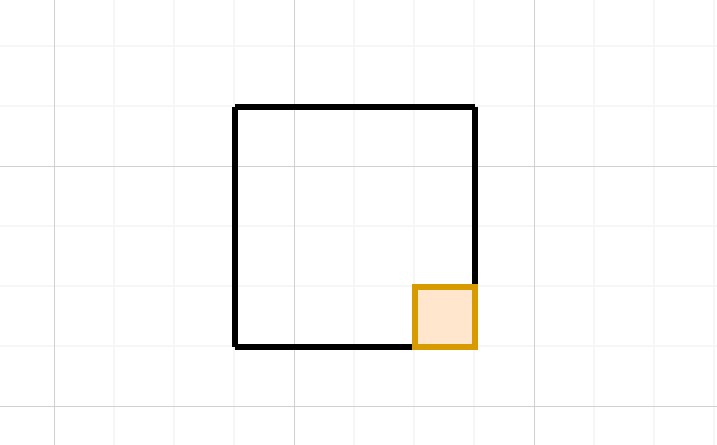
如圖,在只考慮普通推箱規則的前提下,當箱子被移動到這樣一個角落當中的時候,它就不可能再被移動了,因爲玩家只能從上方或左方推動箱子,而箱子的下方和右方又都是牆,阻止箱子的移動。
同理,我們可以考慮如下變體:
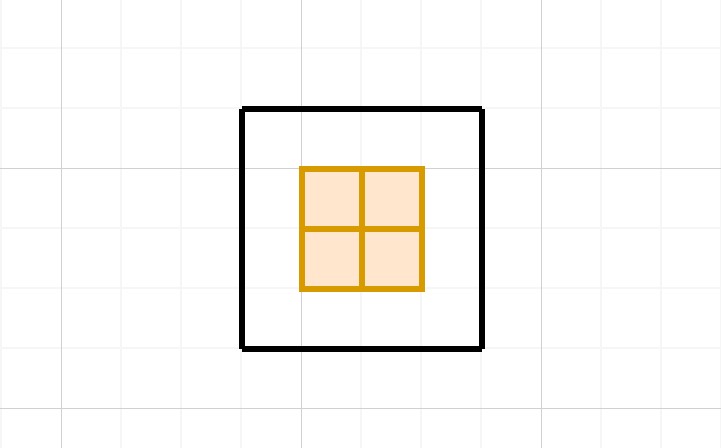
在普通推箱規則中,玩家是不能一次性推動多個箱子的,所以在上面的情況下,四個箱子中的每兩個對角箱子都形成了讓另兩個箱子無法移動的“角落”,因此從整體上來說,這四個箱子的位置已經固定了。
舉這個例子是爲了說明,對於這樣的邏輯結論,將普通的底層推理推廣到更廣泛的情況也是一種非常重要的思路,這樣可以讓你“舉一反三”,讓你可以想象更多類似的情況,比如下面這個情況:
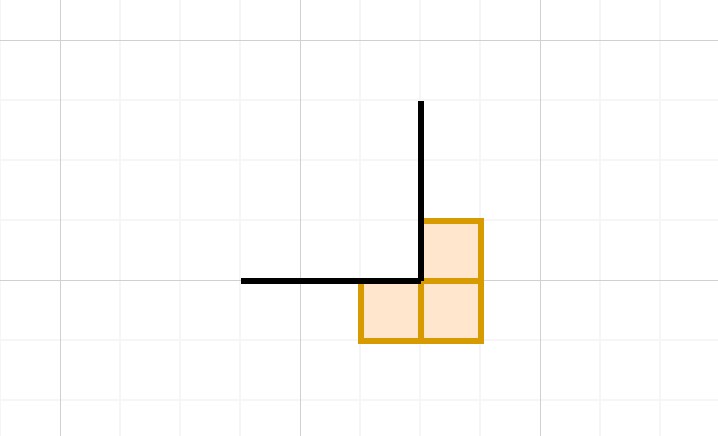
無非就是把上面的情況中的一個箱子換成了牆,並不會影響具體的效果。
通過這樣的高級結論來發現什麼能做(瓶頸步驟)以及什麼不能做(失敗狀態)可以帶來非常高的成就感,但在運用時也需要非常注意如下事項:
你有沒有真的“證明”出一個更廣泛的結論?該結論是不是隻在特定情況或條件下成立?
在新機制/新交互加入後,你的結論是否仍然成立?
如果不多加註意,有可能會因爲“僞證”而錯過正確的可能性,甚至有可能得出更多根深蒂固的錯誤結論,最終導致卡關。所以在得出這樣的結論之前,一定要謹慎再謹慎。
中場休息
以上就是我目前能想到的主要策略,我只挑了這種大方向來說,如果將話題拓展到各種各樣具體的推理方法,那就有點太長了,而且會顯得很亂。也歡迎大家在評論區分享自己的見解!
那麼接下來,我會舉幾個具體謎題的例子,用來說明上述這些策略在解謎中是真的有用。
案例一:Microban 1
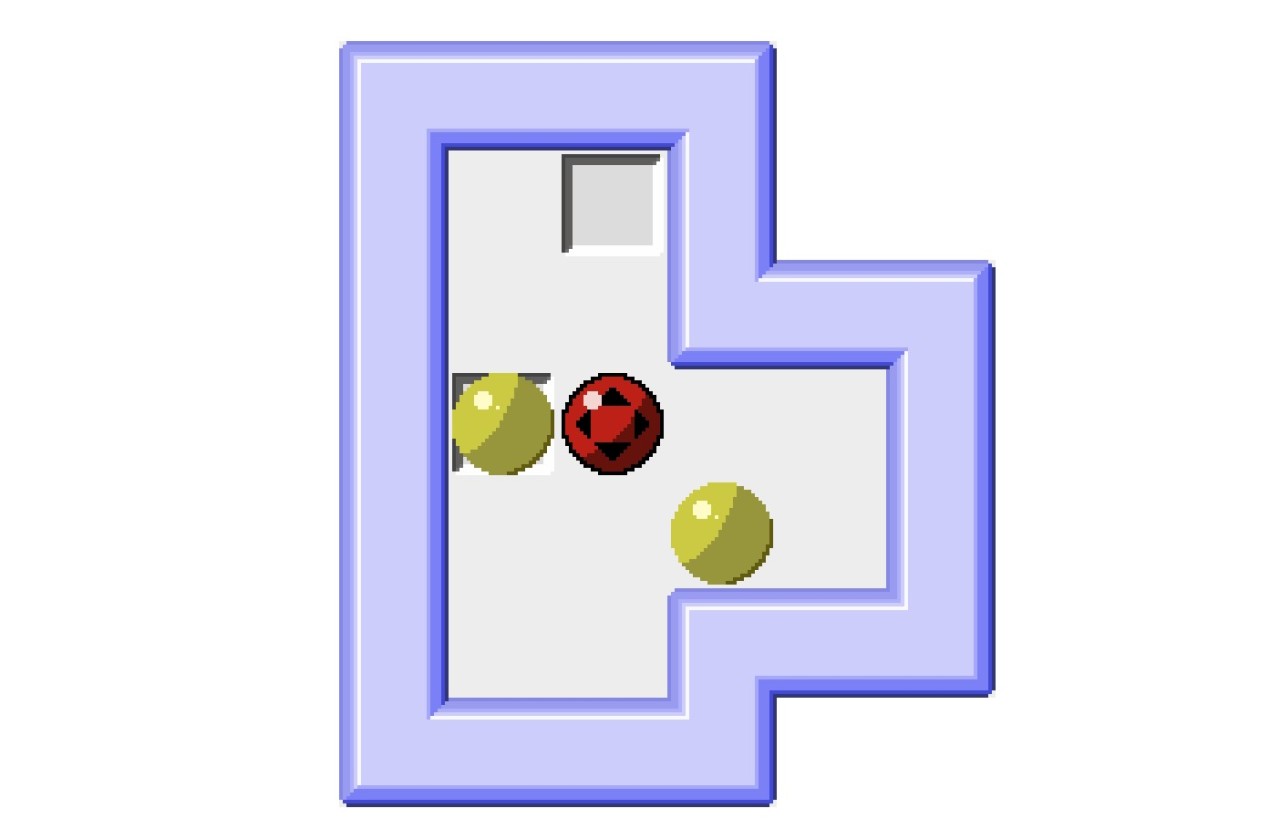
Microban是由David W. Skinner設計的極簡純推箱謎題集(可以在itch.io上搜索),其中的第一個謎題(上面截圖中的謎題)已經成爲了Thinky解謎圈內的經典梗。在上面的圖片中,紅色的是可操縱的主角,黃色是“箱子”,而方形的是箱子要被推到的目標。雖然對於推箱老手來說,這個謎題隨隨便便就可以做出來,但是用它來演示老手背後可能的邏輯過程,我覺得非常合適。
爲了方便描述,將目標格和箱子標號如下(易得該狀態和上面狀態等價,可以互相到達):
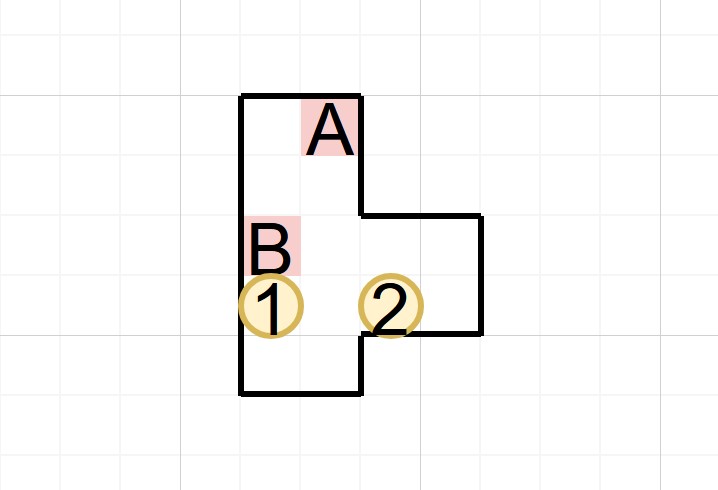
首先我們可以立刻倒推:在最終狀態下,兩個箱子要分別到達兩個目標格,可是每個箱子分別對應哪個目標格呢?利用一個簡單的高級結論——箱子1在這種情況下不可能離開左邊牆壁——我們可以立刻得到,目標A只能由箱子2來到達(因爲箱子1到不了),那顯然目標B就和箱子1對應了。
根據這一點,我們進一步發現一個瓶頸步驟:箱子2必須要從右邊的凹陷當中出來。它不能往右,因爲會卡死在角落裏,也不能往下或往上,因爲有牆堵着,所以唯一的方式就是往左。在箱子2向左後,它不能向左或向下卡在角落裏或者左邊的牆上,也不能向右回到本來的位置,要不然剛纔那一步就沒意義了,因此之後只能向上。
於是具體而言,我們需要先將箱子2向左推,然後幾乎立刻將箱子2向上推,讓我們具體考慮一下這個情況:
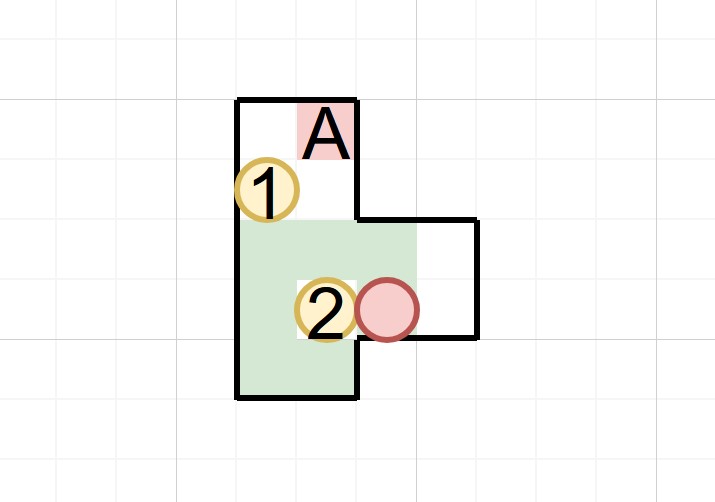
先忽略箱子1的位置,單純看主角(紅色圓)在向左推箱子2之後,又要把它向上推,中間需要經過哪些格子,顯然是圖中綠色的那些位置。那如果已知這些格被佔用、箱子1不能卡在角落、箱子1不能離開左邊牆壁所有這些結論,那麼箱子1在這個狀態下只能有一個可能的位置,那就是上圖中箱子1的位置。那麼這個瓶頸狀態就被完全確認下來了,這個狀態必須被經過,而且在將箱子2向上推之後的下一個狀態是:
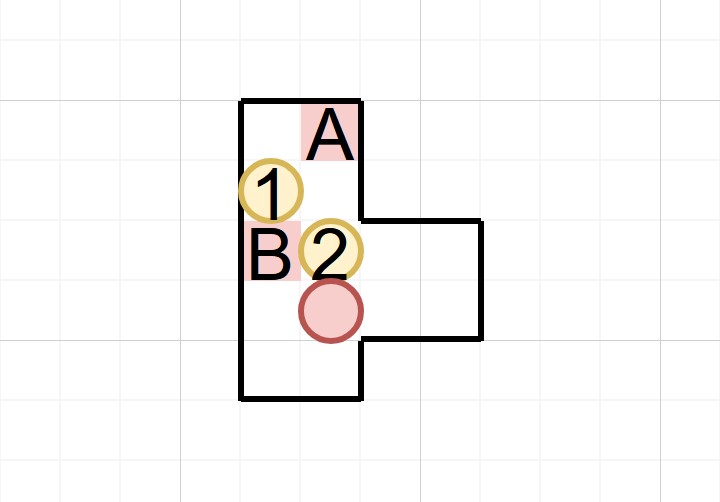
顯然,如果箱子2不移動的話,主角只能把箱子1推進角落卡死,那麼再考慮其它方向,箱子2最終只能向右再次進入凹陷,但此時已經和之前的狀態有本質不同了,不用擔心重複。之後就很簡單了,把箱子1和2依次推到位即可。
對於推箱老手來說,處理這些邏輯基本上就是一瞬間的事情,我只是把這些邏輯表達了出來,所以看上去很複雜,但只要熟悉這種思考方式,多加練習,不消多時,你也能夠成爲“推箱大佬”。
接下來舉一個更加困難的例子,來自一款我最近剛剛開始玩的解謎遊戲:
案例二:Only Sliding某謎題

遊戲:Only Sliding
這款遊戲出自《Recursed》的作者,據說只包含“滑行”機制,所謂“滑行”機制是指,玩家可以操縱一些塊進行移動,但每一次移動,塊都會朝這個方向移動到撞上什麼東西爲止,就像在冰面上“滑行”一樣。
根據我目前的體驗,這個遊戲當中的謎題確確實實就是純粹的滑塊挪移,難度很高,但這並不代表它的謎題設計不好,相反,很多謎題仍然可以通過邏輯推理得到很多有用的結論,減少需要試錯的可能性。
這裏要舉例的是這款作品的一個前期謎題,不在上面的截圖中,但如果只是展示題面的話也不涉及什麼劇透。爲了方便,我直接畫了張示意圖:
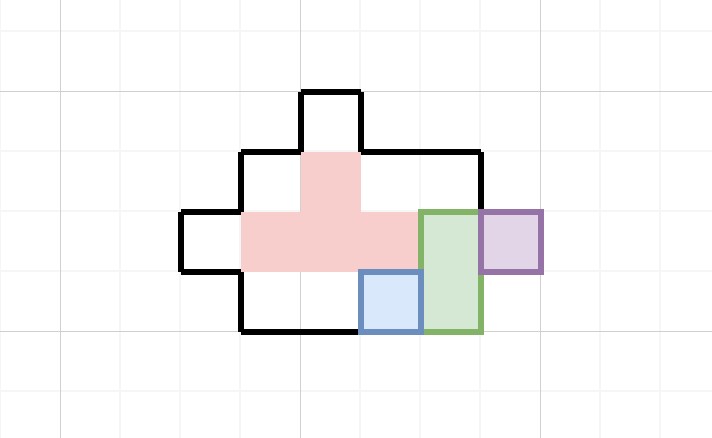
圖中的紅色部分是過關的目標位置,黑色的邊框是不可移動的牆,而右下角的三個不同顏色的塊就是要被玩家操縱到達目標位置的幾個塊,玩家一次只能操縱一個塊移動。
首先倒推,顯然過關狀態是下面這樣(兩個1x1的塊可以互換位置):
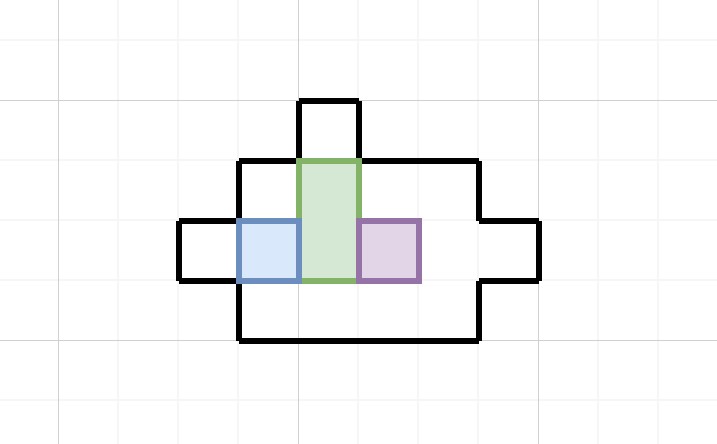
注意到,在過關狀態中,兩個1x1的塊都位於謎題從上到下第三行,但初始狀態並不是這樣的(藍色的塊在第三行外),所以必須存在一個瓶頸步驟,讓兩個1x1的塊全部進入第三行。第一個1x1的進入有很多方法,但在這裏非常值得考慮的是,第二個1x1是怎麼進入第三行的。
此時,由於第一個1x1已經進入第三行,那麼用它來把第二個1x1墊進第三行就是不可能的,而第二個1x1又顯然不可能純靠自己和關卡邊框進入第三行,因此只有一個結論:第二個1x1需要通過墊在1x2的塊上進入第三行。
不難發現,1x2塊和第二個1x1塊在某個瞬間一定會形成下面這個佈局(先不考慮第一個1x1塊的位置,只需要知道它在第三行就好):
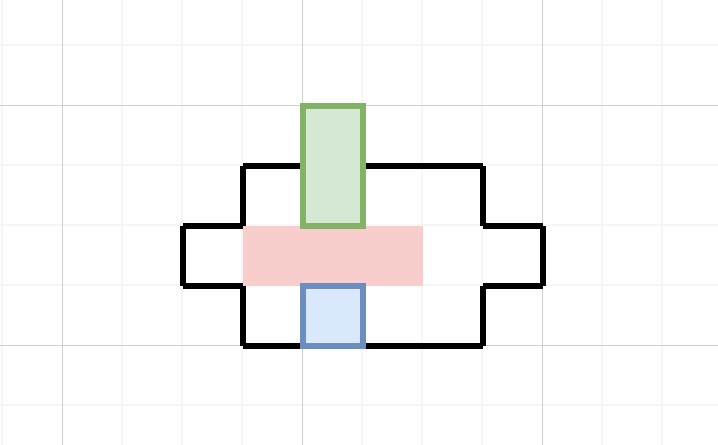
然後1x1的塊向上移動,就此進入第三行。這就是關鍵的瓶頸狀態。
那麼現在先考慮怎麼到達這個瓶頸狀態,我覺得這是這個謎題裏最難的部分。將這個狀態看作目標狀態,我們可以再次倒推:在來到這個狀態之前,上一步是哪個塊在動?
已經在第三行的1x1塊不可能,因爲就算能動,它也只能在第三行來回動,對我們的分析沒有幫助;有沒有可能是另一個1x1塊呢?如果1x2塊已經在現在這個位置,另一個1x1塊在第三行,那麼這個1x1塊不可能被墊到這一格,除非從上面一格往下,但那個狀態反倒是我們最終要到達的狀態,這樣做是倒反天罡,所以不行。那麼就只剩一個可能:上一步移動的是1x2塊,而且是從下往上移動進上面的凹陷的。
再往回推,你會發現這一步的再上一步,動的也必須是1x2這個塊,而且是向左/向右到達這個位置的,那麼此時,已經在第三行的1x1必須負責墊住它,那麼這個塊的位置應該在哪裏,我們心裏就有數了。就這樣一步一步往回推,具體情況具體分析,外加合理範圍內的嘗試,就可以得到一條非常誇張的邏輯鏈條。如果你想要確認一下,下面是之前最近的一個瓶頸狀態:
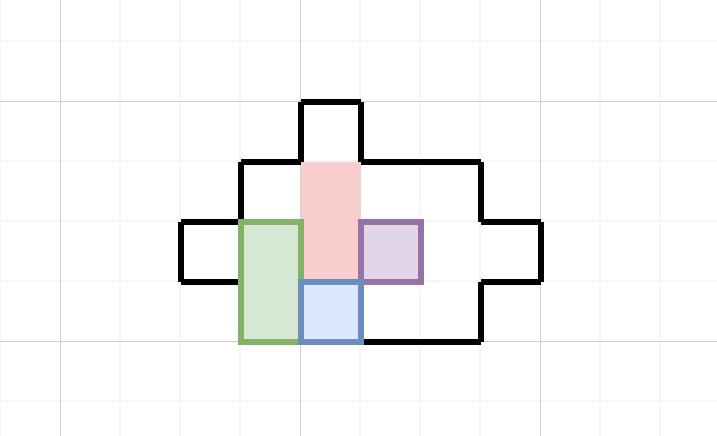
從這個狀態開始移動1x2的塊就可以到達上面的狀態。再往前我就不舉例了,大家應該已經明白意思了。而從最一開始的瓶頸狀態開始,如何到達最終狀態,也可以使用類似的思路解決。這個階段的核心問題是如何讓1x2在縱向上到達正確的位置,而既然兩個1x1塊都已經在第三行,那就不可能拿它們來墊住上面或者下面,所以只能通過牆壁到達正確的縱向位置,然後再橫向墊到1x1塊上,這裏我就不再贅述了。
這樣的謎題正是因爲只有這麼一條由各種各樣的“瓶頸狀態”連接而成的前進道路,所以如果純純靠試,基本是不可能做得出來的。除非你大腦爆算能力真的非常強(
結語

遊戲:Lab Rat(即將發售)
如果想的話,我還可以舉出好多好多的例子,不管是不是推箱子,但現在就到這裏吧,如果大家還感興趣的話,我也可以試試找找其它例子進行分享哈哈
雖然必須要說的是,並不是所有邏輯解謎遊戲都“支持”這樣的邏輯思考方式,但我覺得優秀的謎題設計不僅僅要做到“有解”,也不僅僅是要做到“很難靠試解出”,而且還要做到“有跡可循”,而其中的一種方式就是鼓勵這種有趣的思維方式:有關空間位置、時間順序等的邏輯推理。當然,不一定需要是這麼嚴謹的邏輯推理,只要能在某種程度上有“可解釋性”即可。在以這種思路爲核心開發的解謎遊戲之中,通過邏輯推理來解決謎題不僅會讓你感到如魚得水,而且這種靠自己解謎的成就感還能再上一層。
而對於那些認爲“這一大堆東西有什麼意義?”或者“玩個遊戲還要這麼累?”的玩家,我並不打算反駁,所謂“意義”和玩遊戲所尋求的“價值”本來就是因人而異,解謎遊戲就是這麼一個需要主動找到樂趣的品類,如果你覺得這太麻煩,那不玩就好了。並不是說玩解謎的玩家智商就比不玩解謎的玩家更高,或者解謎遊戲的價值就一定高於其它遊戲的價值。如果你有看到有解謎玩家表現出這樣的“優越感”,請你清楚我和絕大多數Thinky解謎社區玩家都不認同這樣的行爲。
不過,我還是很希望我的這些文字能夠爲更多對解謎感興趣,但是卻苦於沒有系統的思維方法的玩家,提供那麼一些幫助。
那麼就說到這裏,我們下次有緣再見!
無獎競猜:從我這篇文章的用詞來看,你可以猜一猜我是學什麼的,我覺得非常好猜了吧哈哈哈
更多遊戲資訊請關註:電玩幫遊戲資訊專區
電玩幫圖文攻略 www.vgover.com













