賺還是虧？幸運福袋中的數學期望與價值可視化

假設：公佈概率爲實際概率，而且同一品質內遊戲抽到的概率相等

在這篇文章中，用史低價格表示遊戲價值

先來看看白銀福袋裏的遊戲價值（我一個一個搜的）

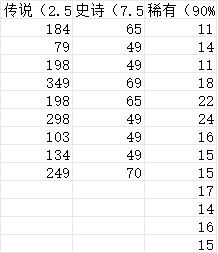
可以看到，傳說級的價值挺高，但稀有級的價值挺低，接下來就可以分析期望了：

# 計算每種品質獎品的平均價值

values_legendary = [184, 79, 198, 349, 198, 298, 103, 134, 249]

average_legendary = sum(values_legendary) / len(values_legendary)

values_epic = [65, 49, 49, 69, 65, 49, 49, 49, 70]

average_epic = sum(values_epic) / len(values_epic)

values_rare = [11, 14, 11, 18, 22, 24, 16, 15, 15, 17, 14, 16, 15]

average_rare = sum(values_rare) / len(values_rare)

# 根據概率加權求和

probability_legendary = 0.025

probability_epic = 0.075

probability_rare = 0.90

weighted_legendary = average_legendary * probability_legendary

weighted_epic = average_epic * probability_epic

weighted_rare = average_rare * probability_rare

# 計算總的平均價值

total_average_value = weighted_legendary + weighted_epic + weighted_rare

total_average_value

結果

23.66111111111111

沒想到的是，白銀福袋裏遊戲的期望居然比售價高！將史低期望再乘0.9表示實際價值，仍然比福袋售價高，（有良心！）這說明如果買很多次，買白銀福袋是划算的。

時間不夠，青銅福袋我就不計算了

接下來看看黃金福袋：

# 計算每種品質獎品的平均價值

legendary_values = [349, 198, 103, 268, 298, 134, 249, 99, 168]

epic_values = [49, 49, 49, 79, 69, 46, 49, 49, 49]

rare_values = [11, 33, 17, 23, 23, 24, 19, 9, 16, 26, 19, 28, 14, 15]

average_legendary = sum(legendary_values) / len(legendary_values)

average_epic = sum(epic_values) / len(epic_values)

average_rare = sum(rare_values) / len(rare_values)

# 根據概率加權求和

weighted_legendary = average_legendary * 0.05

weighted_epic = average_epic * 0.25

weighted_rare = average_rare * 0.70

# 計算總的平均價值

total_average_value = weighted_legendary + weighted_epic + weighted_rare

total_average_value

結果

37.772222222222226

驚不驚喜，意不意外？這個結果其實再乘以0.9比較合理（遊戲價值比史低略低），也就是34元左右。期望比福袋售價多了5元！相比白銀福袋，顯然買黃金福袋更划算些。（）

爲了更加直觀的表現數據，給大家看看這個圖：（黃金福袋的遊戲史低數據）

橫座標表示累積概率，縱座標表示遊戲價值（起點是10元）

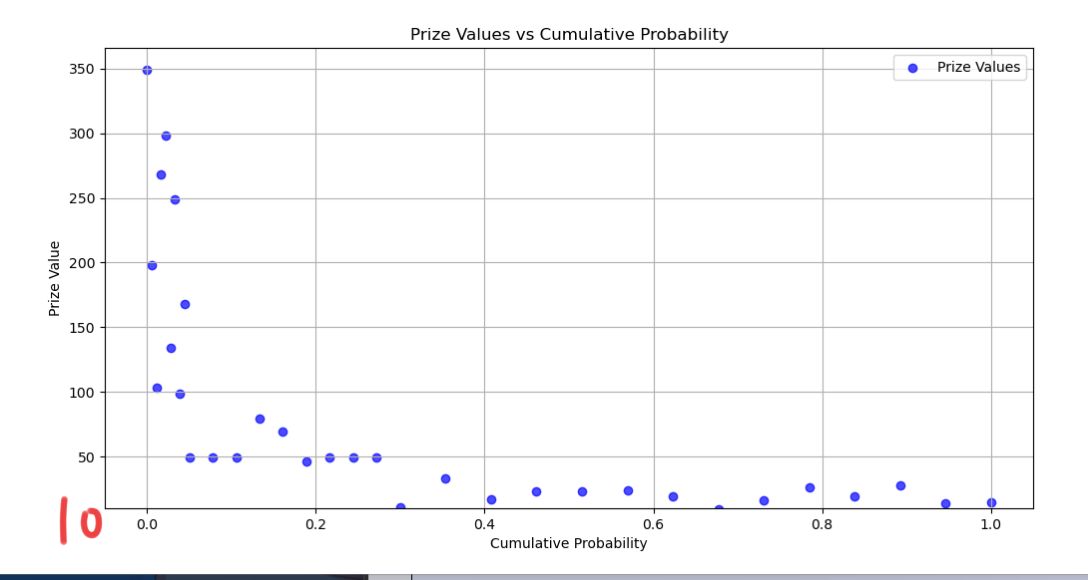
但是可以看到，超過30元的概率算是小的了，數學期望大不代表更容易抽到高價值的遊戲！！（重要提醒）如果只抽一兩次，虧是很可能，賺說明你是歐皇

以上就是全部內容了

求贊求贊