张益唐——黎曼猜想，华人数学家再创重大突破！

11月5日，华人科学家张益唐教授，在山东大学分享了他最新的学术成果，论文主题为朗道-西格尔零点猜想，该猜想主要解决广义黎曼猜想中L函数是否存在异常零点的问题，张益唐本人相当自信，预计论文在同行评审通过后，将成为数学史上又一里程碑的突破，而且会比张益唐在孪生素数猜想上的成就意义更大！

七大难题

黎曼猜想，是波恩哈德·黎曼在1859年提出的，接近200年的时间里，黎曼猜想成为数学家最感兴趣，同时也是数学界最重要的问题！在千禧年之际，麻省剑桥市的克雷数学研究所，选出了七个“世界难题”，每个问题都象征性地悬赏一百万美元。

“七大难题”包含NP完全问题、庞加莱猜想、杨-米尔斯存在性和质量间隙等难题，黎曼猜想正是其中之一。在此之前，普遍科学家认为广义黎曼假设预计是正确的；截至目前，已经有上千条数学命题是以黎曼猜想的证明作为前提存在的，那么黎曼猜想与本次张益唐教授的成果有何关系呢？

朗道-西格尔零点猜想（Landau-Siegel Zeros Conjecture），是黎曼猜想的某种弱形式，通常也被视作黎曼猜想的核心问题，如果论证这个所谓的朗道-西格尔零点不存在，那么上千个数学命题将直接晋升为公理；若零点存在，那么将与黎曼猜想产生冲突......

素数

1859年8月，32岁的数学家黎曼，向柏林科学院提交了一篇论文，题目为“论小于一个给定值的素数的个数”，短短八页的论文中的猜想成为后世数学家奋力解决的问题，文中黎曼所探究的问题其实相当相当简单，只需要小学三年级学生就能看懂，黎曼抛出问题：小于20的素数有多少个？

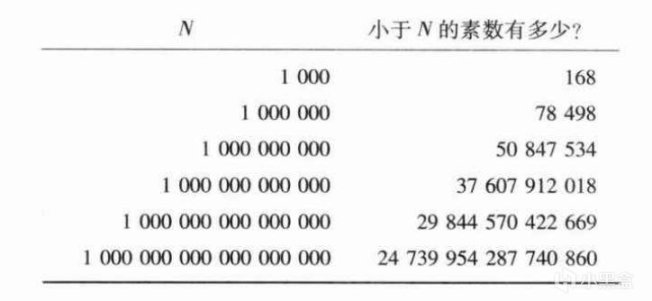
答案是8个：2，3,5,7,11,13,17和19。黎曼继续发问，小于1000的素数有多少个？小于100万呢？小于10亿呢？尽管我们今天的超级计算机轻松给出答案，小于1000的有168个素数，小于100万有78498个，小于10亿的有50847534个，数学家高斯则亲手统计过300万以内的素数，但我们依然需要一个普遍的规律或公式，来确定素数的分布情况。

黎曼提出了对这个问题的一个猜想，然后附文写道，“人们当然希望对此有一个严格的证明，但是我稍稍做了一些徒劳的尝试后，便把寻求这样一个证明的事搁置一边，因为它对于我目前的研究工作并不是必需的”，恰恰是这个不算太起眼的猜测，成为数学界最重要的谜题，这个猜测日后被称为“黎曼假设”/“黎曼猜想”。

素数定理

讨论素数，我们很容易发现自然数越靠后的数字，素数出现的频率似乎越低，经过简单统计，1到100之间有25个质数；401到500之间有17个；901到1000只有14个；像这样每隔100个整数取一次，一直列到10000亿，最后一组百数段里仅有4个素数。如果这样一直到万亿万亿万亿万亿，最后在某一个地方之后素数会不存在吗？

这个问题早在公元前300年，欧几里得就已经给出了相当完备的证明，他认为素数永远不会稀疏到没有，即没有最大的素数——素数无限定理，欧几里得假设从p1开始一直到pn均为素数，最大的素数为pn，构造一个s = (p1 x p2 x p3 x ... x pn) + 1 的数，若s为素数，那么s>pn与假设矛盾，若s并非素数，那么s不能被已知最大的素数整除，同样矛盾。

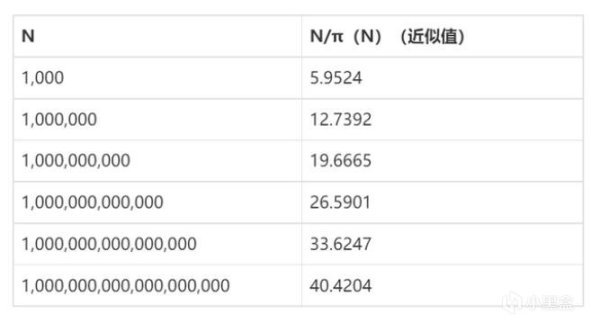
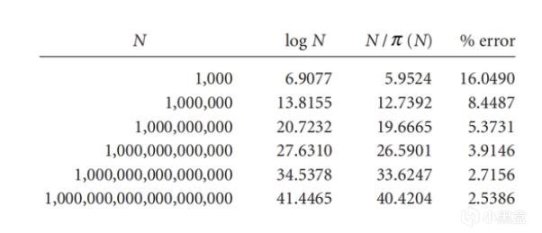
已知素数有无穷多个，再来考虑素数的分布问题，上面我们用π(N)来表示“小于（等于）N的素数个数”，再简单用N/π(N)，得到了一组似乎是以7为公差的等差数列，这仅仅是巧合吗？我们再将对数log N对比列出来，可以发现，当N越大的时候，N/π(N)越接近log N。

黎曼ζ函数

有了这一发现后，我们按照欧拉使用的数学符号得到上面的素数定理，接下来的内容则涉及到高数/数分，我们从调和级数开始入手，调和级数可以简单理解为调和数列（各项倒数为等差数列的级数）各元素之和，可以通过Cauchy判别法判断，所有调和级数都是发散的（Divergent）。

原本的调和级数如下式，即1,2,3,....各项倒数所成的数列，我们继续推广，1,2,3,....平方的倒数所组成的数列，即级数1+1/4+1/9+1/16+...，欧拉给出了极限为π^2/6，即自然数平方倒数之和等于π^2/6，每一个初次看到这个证明的人都会为数学的神奇震惊不已，我们继续推而广之。

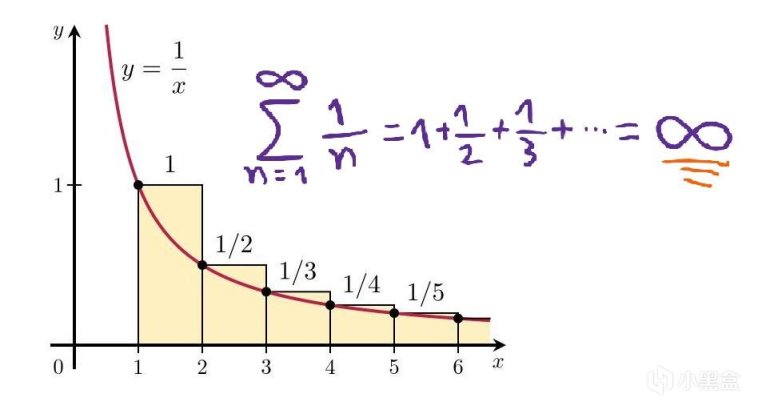
将调和级数推广到下面的ζ函数（Zeta Func），上面自然数平方倒数之和可以理解为ζ(2)，上面第一段的调和级数ζ(1)→∞，欧拉继续证明ζ(2)=π^2/6，最终在1737年发现欧拉乘积公式，初步探究到ζ函数与素数存在某种关系，黎曼进一步思考，如果ζ函数里的s均为素数呢？

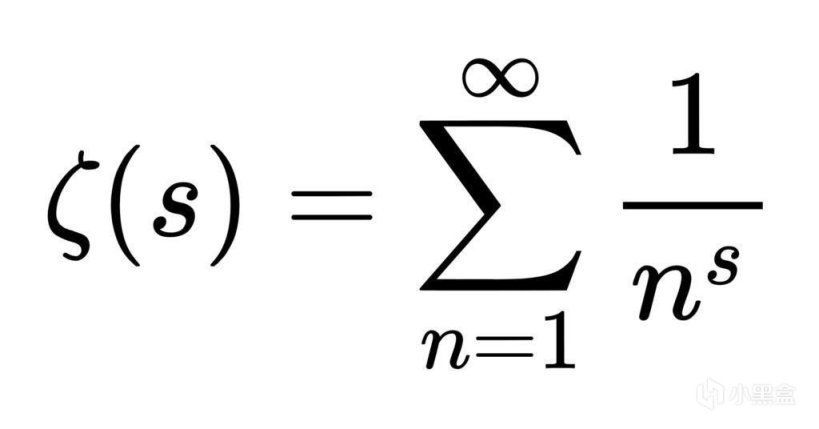
黎曼猜想

黎曼研究的领域极广，同时也是复分析的创始人之一，他发现如果从复平面上思考Zeta函数，会出现很有意思的变化。复平面上X轴对应实部，Y轴对应虚部，将复数输入ζ函数，发现仅有在实部大于1的情况下级数才收敛。原有的ζ函数只满足实部 Re(s) > 1的情况，黎曼于是进行了“解析延拓”。

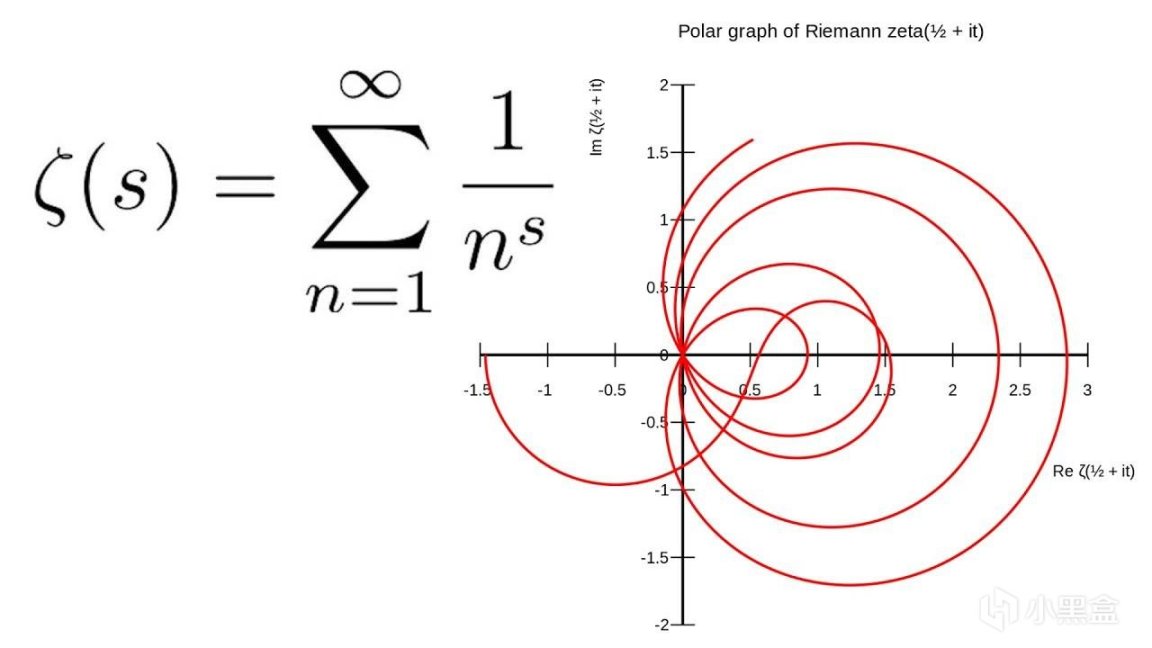
这部分的可视化可以参考3B1B的视频，黎曼对欧拉的ζ函数进一步推广到复平面，即填补Re(s) < 1的函数，使得黎曼ζ函数同时符合欧拉常规的s与复平面上的s，下图中左半部分即为解析延拓的可视化，它们不是被求和算出来的，而是通过解析延拓证明出来，且具有唯一性，当s=-1时，我们可以得出ζ(-1)=-1/12（注：该式非自然数和）。

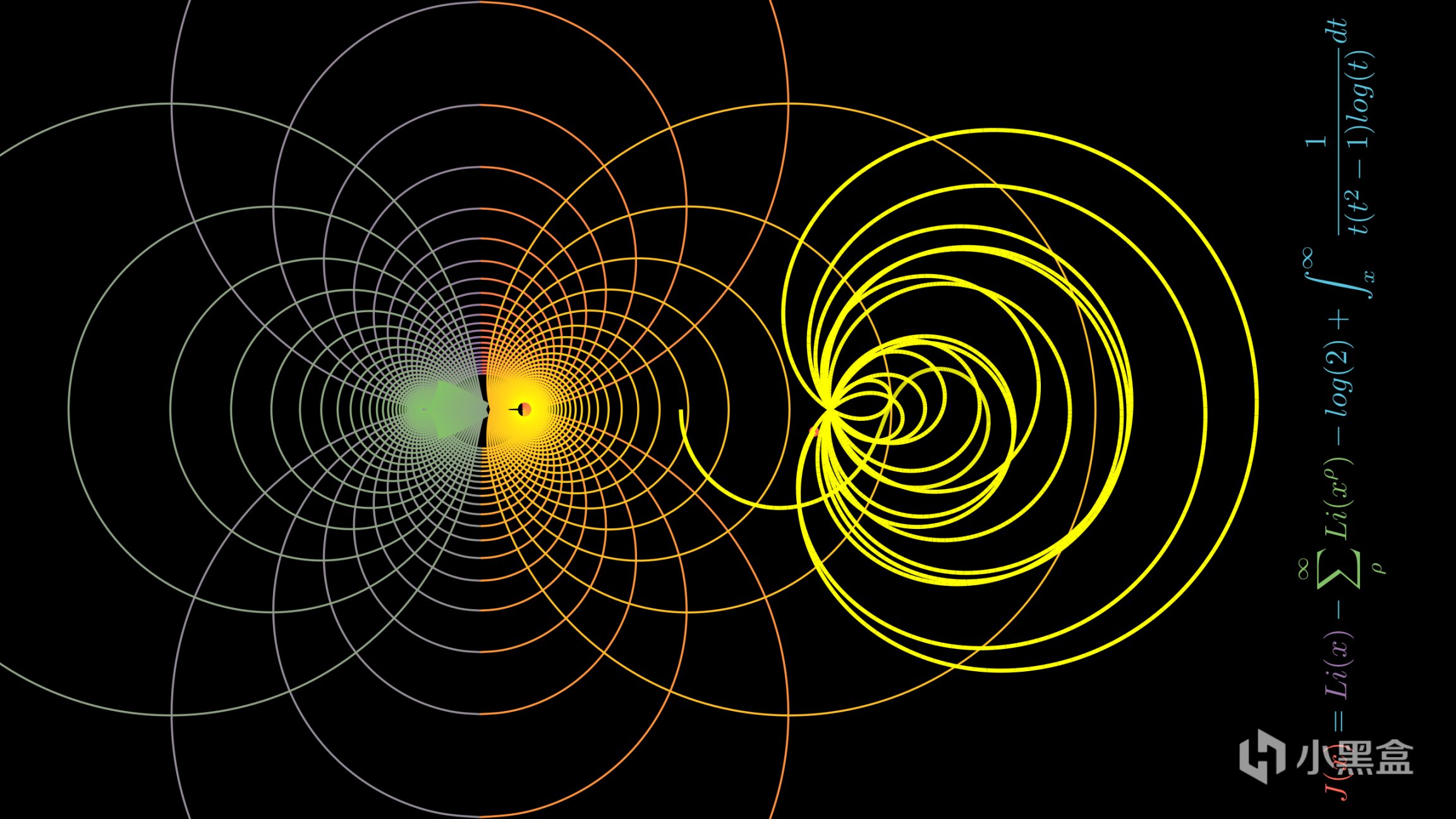
有了以上基础，我们推导出黎曼ζ函数满足以下代数关系式，我们发现当S=-2n时ζ为零，我们将其称为黎曼ζ 函数的零点，这一部分零点分布有序，我们将其称为平凡零点 (trivial zero)，其他零点则称为非平凡零点，黎曼给出猜想是，黎曼ζ函数的所有非平凡零点，都位于复平面上 Re(s)=1/2 的直线上，即实部=1/2的轴上，换句话说，方程ζ(s)=0的解的实部都是1/2。

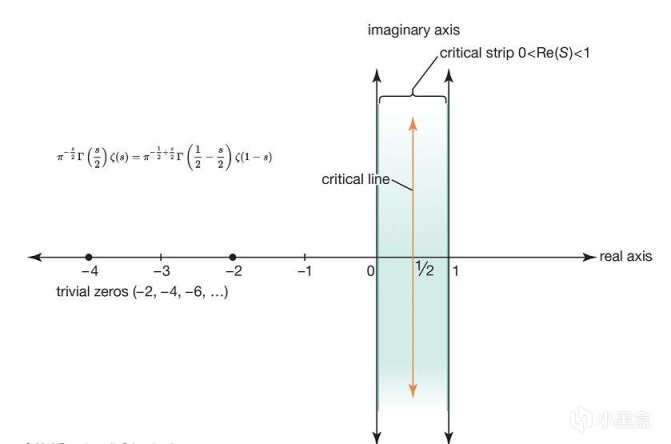
朗道-西格尔零点猜想

黎曼猜测Zeta函数所有非平凡零点都在实部1/2的直线上，此后多位数学家在黎曼ζ 函数的基础上不断打“补丁”，到了十九世纪，数学家狄利克雷引入L函数，相信很多人都听说过狄利克雷定理，即对于任意互质的正整数a,d，有无限多个形式如a+nd的素数。

于是描述狄利克雷L函数的黎曼猜想被称作广义黎曼猜想（GRH），原问题从黎曼ζ 函数非平凡零点都在实部1/2的直线，变成L函数的非平凡零点都位于1/2直线上，西格尔给出ξ函数数值的计算方法，他与老师朗道一起发现了L函数理论中的零点现象，并且确定非平凡零点基本上落在类沙漏的区域，此前Atiyah爵士曾自称证明了黎曼猜想，而张益唐在07年曾给出过L函数非平凡零点的下界估计。

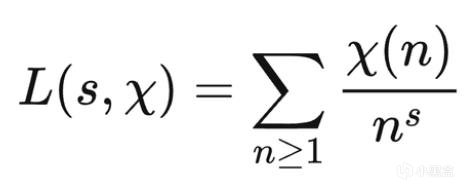
但当时的理论还存在瑕疵，于是张益唐13年在孪生素数方向取得突破性研究，确立了存在无穷多差小于7000万的素数对，有了这一基础，22年的菲奖得主詹姆斯·梅纳德对孪生素数继续进行优化；今天张益唐的新论文也是抛出了L函数在1处的下界(log D)^(-2022)，这里-2022也相当具有代表意义，如果方法成行，那么有机会像孪生素数那样继续优化，直到L函数要求的-1。