“数学界诺奖”！日本数学巨匠柏原正树，成亚洲首位获奖者！

本周，2025年的阿贝尔奖得主正式公布，78岁的日本京都大学教授Masaki Kashiwara（柏原正树），凭借在代数分析和表示论领域做出的基础贡献（特别是D-模理论和晶体基领域的开创性成就），拿下了号称数学界诺贝尔奖的阿贝尔奖，也成为首位来自北美、欧洲或以色列以外地区的获奖者。

01 数学三大奖

数学，作为全世界自然科学最重要的基础学科之一，深刻影响着人类文明进程的发展，为了表彰数学家们的卓越贡献，国际数学界设立了多项权威奖项，其中以菲尔兹奖、沃尔夫数学奖、阿贝尔奖最为瞩目，被称为“数学三大奖”。

前不久中国数学家王虹凭借对挂谷猜想这一世纪难题的证明，成为菲尔兹奖的热门候选人之一，菲奖在1936年首次颁发，由加拿大数学家约翰·查尔斯·菲尔兹倡议设立，旨在奖励40岁以下青年数学家的杰出成就，每四年颁发一次，截至2022年，全球仅65位数学家获此殊荣，包括华裔数学家丘成桐和陶哲轩。

沃尔夫数学奖于1978年设立，是沃尔夫奖六大分支之一，不设置年龄，每年颁发一次，旨在表彰对人类科学与艺术文明有终身贡献的数学家。这次的阿贝尔奖是设立时间最晚的一个奖项，于2003年由挪威设立，主要为了纪念数学家尼尔斯·阿贝尔，每年颁发一次，无年龄限制，奖金达700万挪威克朗（约合500万人民币）。

02 阿贝尔奖

菲奖注重表彰年轻数学家，阿贝尔奖则是完全对标诺奖，由挪威科学与文学院负责评选，主要就是为了填补诺奖没有数学奖的遗憾，截至2025年全球共有29位数学家获得这一奖项，获奖者平均年龄为76岁，主要体现阿贝尔奖对终身成就的重视。所以说虽然菲奖有年龄限制获奖难度更大，但是如果对标诺奖终身成就表彰这个级别，还是阿贝尔奖更有代表性。

在阿贝尔奖29位获奖者中，数论、代数几何和微分方程是获奖成果最集中的方向，也是现代数学最前沿的发展趋势，阿贝尔奖表彰数学家所取得的那些成就，也对全世界产生了深远的影响，比如约翰·纳什，他凭借对非线性偏微分方程研究，在2015年获得阿贝尔奖，而纳什在博士论文中提出的纳什均衡，获得了诺贝尔经济学奖，成为至今唯一一位同时获得诺奖和阿贝尔奖得主的数学家（比较遗憾的是纳什从挪威领取阿贝尔奖后，从机场回家的途中遭遇车祸身亡）。

今年阿贝尔奖得主柏原正树同样也有类似的经历，他在23岁硕士论文中，就早早提出了D-模理论的雏形，不仅有开创性的成果，同时也极其高产，阿贝尔奖的颁奖词写道，“50多年来，柏原正树重塑并极大丰富了代数分析和表示论领域。他的工作已成为几代研究员的灵感源泉！”接下来一起看看这位大师的传奇经历和学术成果。

03 柏原正树

柏原正树（Masaki Kashiwara）1947年1月30日生于日本茨城县结城市，小时候痴迷“鹤龟问题”（通过头与腿的数量推算鹤与乌龟的数量，类似于我们的鸡兔同笼），自幼展现出对数学的浓厚兴趣。1969年，柏原正树获得东大数学学士学位，1971年完成硕士学业，师从日本代数分析先驱佐藤干夫（Mikio Sato）。

硕士论文首次将代数工具系统引入微分方程研究，奠定了D-模理论（D-module）的基础。1974年，柏原正树在京都大学获得博士学位，毕业论文中利用D-模理论与奇点分解，证明了伯恩斯坦-佐藤多项式（b函数）根的合理性，进一步拓展了代数分析的边界。

1978年起，柏原正树长期任职于京都大学数理解析研究所（RIMS），历任教授、特任教授，柏原正树曾经在1978年与1990年两次受邀在国际数学家大会上发表演讲，成为日本数学界的重要代表之一，2010年退休后仍以名誉教授身份持续研究，专注于单子范畴（monoidal categories）等前沿领域。

04 D模理论

柏原正树这次获奖的主要成果之一就是D模理论（D-module theory），属于代数分析中的核心分支、与微分方程的交叉领域，D-module中的D就是微分（Differential）的意思，微分大家在高中竞赛或者大学都学过，D模理论最简单用一句话解释，就是用代数方法来研究微分算子的结构与微分方程的解空间，D-模就是微分算子环（D-环）的模。

具体来说，D-module中的D代表微分算子（Differential Operator），是一种抽象出来的数学工具，通常表示就是D或者d/dx，作用就是对函数进行微分运算，比如对于可微函数 f(x)，一阶微分算子的作用定义为D[f(x)]=df(x)/dx，高阶微分算子则通过多次复合实现，也就有了乘积法则、链式法则这些基础概念。

在代数分析中，D-环通常是指一个流形上的微分算子环，这里的环（Ring），再加上环、域，都属于抽象代数中最基础的专有结构，比如这次柏原正树得的阿贝尔奖，就有以阿贝尔为名的阿贝尔群。简单来说，环就是符合两个二元运算（通常称为加法和乘法）的一个集合。

05 延伸阅读（黎曼-希尔伯特对应）

比如整数Z配备了普通的加法和乘法，就是一个有单位元的交换环，实数R和复数C也是有单位元的交换环，多项式R[x]也是同理，mxn矩阵集合在矩阵加法和乘法下也形成一个有单位元的环（但通常不是交换环）。再进一步，群的范围更基础，是仅含一个二元运算的集合，阿贝尔群就是符合特定运算性质（交换律）的群，比如整数加法群 (Z, +)就是一个阿贝尔群。

D-module后面这个module模也是一个重要概念，理解起来会比较抽象，与大家学过向量空间类似，向量空间由集合 ( V ) 组成，配备了向量加法和标量乘法两种运算，向量空间的标量来自一个域，比如常见的实数域R或复数域C，R^n就是一个典型的向量空间，而模的标量来自一个环，比如整数环Z 或多项式环R[x]，所以模比向量空间的应用还要更加广泛（两者本质都是阿贝尔群）。

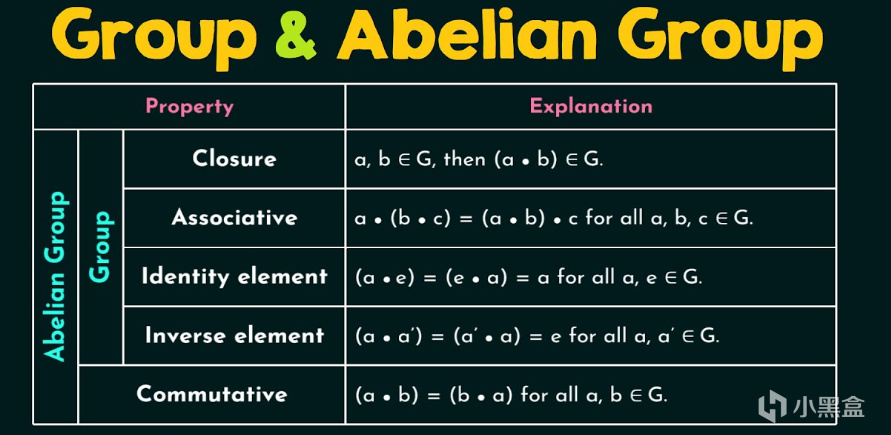
阿贝尔群性质

D-module就是借鉴了这些代数思想，将微分方程转化为代数化模型，D-模也是一个在微分算子环上定义的阿贝尔群，它的标量来自微分算子环，例如在欧氏空间R^n上，微分算子环包含偏导数运算符（比如∂/∂xi）以及它们的多项式组合。根据性质还可以对D-模进行分类，比如与有限维向量空间类似的Coherent D-模（Coherent D-modules）和正则D-模（D-modules with regular singularities）。

柏原正树在1980年将微分方程系统在复流形奇点附近的“单值性”行为转化为代数结构的分析，利用D-模理论证明了高维黎曼-希尔伯特对应（Riemann-Hilbert correspondence），在经典复分析中，黎曼-希尔伯特问题关注如何在复平面上找到具有特定单值行为的解析函数或微分方程的解，随着数学的发展，黎曼-希尔伯特对应被推广到高维复流形上，涉及偏微分方程的研究，这时需要引入更复杂的数学工具，例如D-模理论和层论（sheaf theory）。

柏原正树建立了复流形上Coherent D-modules与可构造层（constructible sheaves）之间的等价关系。具体来说，在复流形上，Coherent D-modules的范畴与可构造层的范畴之间存在一一对应，也就是上文提到的高维黎曼-希尔伯特对应，这个对应将微分方程的解空间（通过D-模描述）与几何对象（如可构造层）联系起来，从而将微分方程的单值化表示与拓扑、几何结构一一对应，为日后研究高维微分方程和复几何提供了强大的代数工具，柏原正树也是因为这一系列的理论获得阿贝尔奖。

06 佐藤干夫

当然，柏原正树这些成就也不得不提到他的老师佐藤干夫，佐藤干夫被誉为“代数分析”领域的奠基人之一，他也是毕业于东大，师从物理学家朝永振一郎，后转向数学研究，1970年起任京都大学数理解析研究所教授，直至退休，佐藤干夫于1958年提出超函数理论，将分布理论推广为更广泛的解析工具，用于描述线性偏微分方程的广义解成为代数分析的基石。

这些成果与格罗滕迪克的层论结合，为后续D-模理论的发展铺平道路，在柏原正树获奖后的采访中，他提到这些兴趣几乎全部来自佐藤干夫。Sato本人在2003年获沃尔夫奖，除了柏原正树外，他还培养了菲奖得主森重文等杰出数学家。

在教学上，佐藤也和一般的教授完全不同，他倡导“数学即宗教”的研究哲学，强调抽象思维与直觉的结合。柏原正树回忆，Sato的教学风格以“禅问答”著称，擅长启发学生去突破技术细节、直抵问题本质，柏原正树认为正是老师的提点才帮助柏原正树逐步走上学术之路，就用佐藤的一句话作为本文的结尾，“真理本就浑然一体，我们不过发现了它的投影。”