常常听说“物理学大厦”的比喻，比如大厦里的这个房间是“热力学”，那个房间是“牛顿力学”，那边那个是“量子力……既然是大厦，那在里面顺便养点可可爱爱的小动物不过分吧？
多年以来，大厦住户众多，因此动物（在对物理学进行讨论的过程中，人们提出的各样载体和假设，算是一种思想实验）也不少，其中相当知名的便是物理学四大神兽——芝诺的龟龟、拉普拉斯妖、麦克斯韦妖、薛定谔的可爱猫猫。
看看老芝
从时间顺序来说，芝诺的乌龟是最早提出的，说是在公元前五世纪，古希腊人芝诺（芝诺的乌龟当然是芝诺提出来的啦，然而洛必达法则并不是洛必达提出的）在阿基里斯前1000米初放了一只乌龟让他去追，在相同时间t内，阿基里斯每跑10s（s>0）米，乌龟就会前进s米，也就是说，阿基里斯跑完1000米的时候乌龟在前方100米，阿基里斯跑完100米的时候乌龟在前方10米处……二者的距离会发生这样的变化“1000—>100—>10—>1—>0.1—>……”，无限趋近于0。
跑得比乌龟还慢（恼）
极限问题
龟人赛跑的故事实在是广为人知，师出同门的河流无限细分悖论听起来则会更加新奇、耐人寻味，现在假如张三要过河，他可以这样看待这个问题：
可以将河流平均分为两等份，先走前面一半再走剩下一半（1/2），而前面一半和剩下一半也都可以被均分，先走前面一半的一半（1/4），而后以此类推（1—>1/2—>1/4—>1/8—>1/16……），这就有了无限分割出来的很小的一半，而每个一半都要相应的时间t，t乘上无穷个一半，不就是无穷吗？
因此张三过河需要的时间是无穷久。
张三：困惑🤔
不是问题
河流问题在理解上比龟人赛跑要抽象，但在实践上却简单得多，因为我们仅凭日常生活的经验就可以知道张三是错的——这是最浅层、最简单的解释。
从运动的属性来看，现实中的运动是连续而自然的，因此并不能用“完成一个时间和空间上无限小的步骤后再完成下一个，直到完成无限个”的模型进行套用，更简单地说，现实中的运动不能进行这样的拆分，我们在数学和物理上只是为了方便计算和精简模型才会这么做的。
从时空本身的性质看，时空本身是可以无限拆分的吗？这似乎和某些量子力学领域的某些假设产生了冲突，倘若时空只能细分到普朗克尺度，那么就根本不会存在“无限分割出来的很小的一半”，它实际上应当是有限的，只不过数量很多而已。
从数学角度来看，这实际上是一个微积分的问题，在已知条件充足的情况下，使用一定的数学技巧就可以算出过河流的时间，提供最直接又客观的答案。
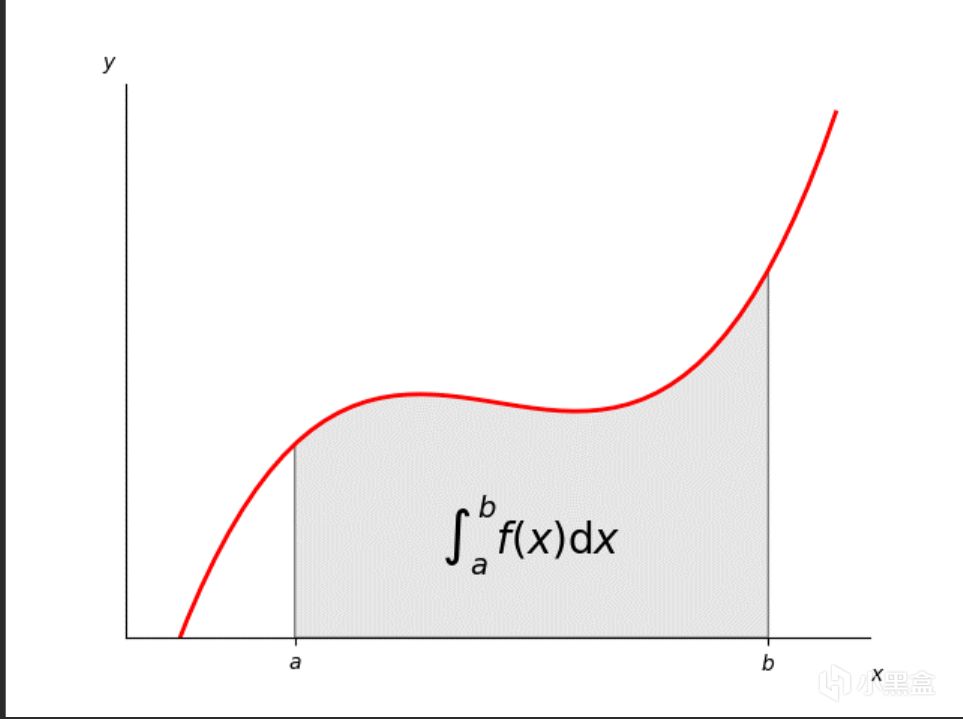
所以为什么过河要用微积分？应该是为了帮助人知其然知其所以然吧，建立一个自洽的科学理论解释问题，然后不断修补、推翻、应用它，大概就是这样的。
更多游戏资讯请关注：电玩帮游戏资讯专区
电玩帮图文攻略 www.vgover.com
