赚还是亏？幸运福袋中的数学期望与价值可视化

假设：公布概率为实际概率，而且同一品质内游戏抽到的概率相等

在这篇文章中，用史低价格表示游戏价值

先来看看白银福袋里的游戏价值（我一个一个搜的）

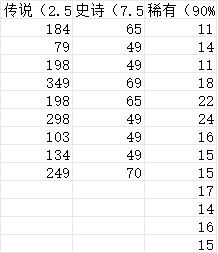
可以看到，传说级的价值挺高，但稀有级的价值挺低，接下来就可以分析期望了：

# 计算每种品质奖品的平均价值

values_legendary = [184, 79, 198, 349, 198, 298, 103, 134, 249]

average_legendary = sum(values_legendary) / len(values_legendary)

values_epic = [65, 49, 49, 69, 65, 49, 49, 49, 70]

average_epic = sum(values_epic) / len(values_epic)

values_rare = [11, 14, 11, 18, 22, 24, 16, 15, 15, 17, 14, 16, 15]

average_rare = sum(values_rare) / len(values_rare)

# 根据概率加权求和

probability_legendary = 0.025

probability_epic = 0.075

probability_rare = 0.90

weighted_legendary = average_legendary * probability_legendary

weighted_epic = average_epic * probability_epic

weighted_rare = average_rare * probability_rare

# 计算总的平均价值

total_average_value = weighted_legendary + weighted_epic + weighted_rare

total_average_value

结果

23.66111111111111

没想到的是，白银福袋里游戏的期望居然比售价高！将史低期望再乘0.9表示实际价值，仍然比福袋售价高，（有良心！）这说明如果买很多次，买白银福袋是划算的。

时间不够，青铜福袋我就不计算了

接下来看看黄金福袋：

# 计算每种品质奖品的平均价值

legendary_values = [349, 198, 103, 268, 298, 134, 249, 99, 168]

epic_values = [49, 49, 49, 79, 69, 46, 49, 49, 49]

rare_values = [11, 33, 17, 23, 23, 24, 19, 9, 16, 26, 19, 28, 14, 15]

average_legendary = sum(legendary_values) / len(legendary_values)

average_epic = sum(epic_values) / len(epic_values)

average_rare = sum(rare_values) / len(rare_values)

# 根据概率加权求和

weighted_legendary = average_legendary * 0.05

weighted_epic = average_epic * 0.25

weighted_rare = average_rare * 0.70

# 计算总的平均价值

total_average_value = weighted_legendary + weighted_epic + weighted_rare

total_average_value

结果

37.772222222222226

惊不惊喜，意不意外？这个结果其实再乘以0.9比较合理（游戏价值比史低略低），也就是34元左右。期望比福袋售价多了5元！相比白银福袋，显然买黄金福袋更划算些。（）

为了更加直观的表现数据，给大家看看这个图：（黄金福袋的游戏史低数据）

横坐标表示累积概率，纵坐标表示游戏价值（起点是10元）

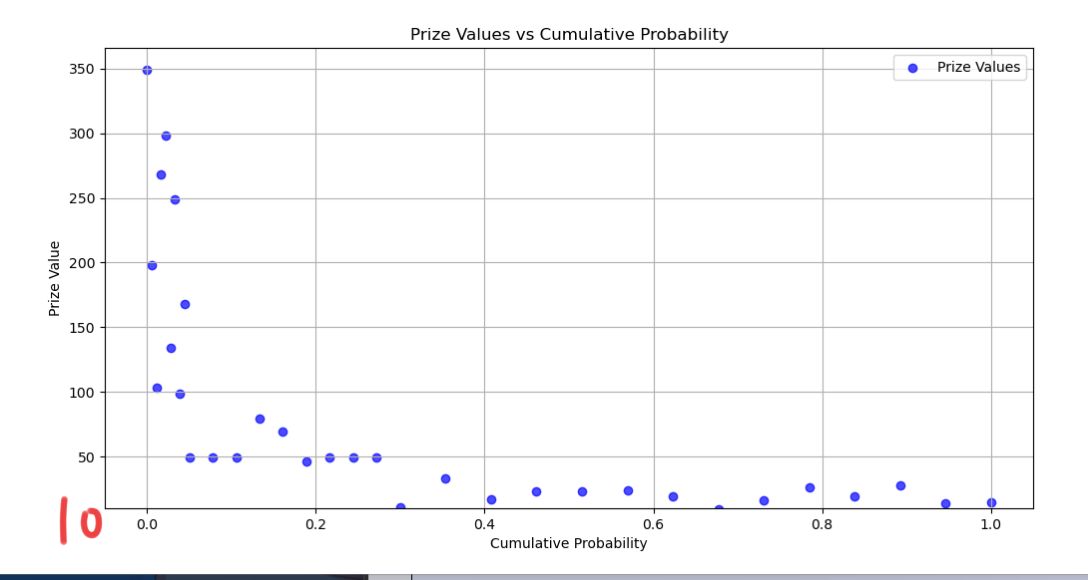
但是可以看到，超过30元的概率算是小的了，数学期望大不代表更容易抽到高价值的游戏！！（重要提醒）如果只抽一两次，亏是很可能，赚说明你是欧皇

以上就是全部内容了

求赞求赞