楼主有个微信群,里面都是一些从小玩到大的好朋友,且里面没有一对情侣,就在楼主以为大家要朋友一生一世的时候,楼主在某一个饭局发现有个女生背着群友在和另一个好兄弟激情私聊
在楼主的狂热追问下,兄弟也承认了对那个女生的好感。这消息对于楼主这位八卦魔王来说简直是惊天地泣鬼神
于是,为了避免错过更多八卦。也为了使得有情人终成眷属,楼主用Python+微信群的聊天记录做了简要的分析~~~旨在找出潜在的暗恋关系

愿天下有情人终成眷属
首先需要的是那个微信群的聊天记录,楼主是根据WeChatMsg这个开源项目去做的,大家可以去Github搜,或者直接在google搜,Github那个页面上有很详细的教程,所以在楼主这里从略~大家有不明白的也可以评论区找楼主~~

导出来大概是这个样子~
楼主这个群半年就产生发了一万多条消息吧~
于是就可以开始打Code啦,最后结果会以热力图体现~~~

楼主的想法是先根据时间信息对时间进行一个聚类,聚类得到很多个不同的话题(比如说按照一段时间没人说话就分成另一个话题)楼主这里用的是密度聚类(按一个小时),盒友也可以尝试下别的聚类方法~,然后再对每个话题进行相关分析~
一、对时间进行聚类形成话题
首先引用一些库
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score
from scipy.stats import pearsonr
然后导入你的数据
mydf = pd.read_csv('你的那个群哈.csv')
Strtime = mydf.StrTime.tolist()
Createtime = mydf.CreateTime.tolist()
dic_time = dict(zip(Createtime,Strtime))
nicknamelst = mydf.NickName.tolist()
dict_name = dict(zip(Createtime,nicknamelst))
nickname= list(dict.fromkeys(nicknamelst))
dic_nameint = dict(zip(nickname,range(len(nickname))))
dic_intname = dict(zip(range(len(nickname)),nickname))
然后聚类
# 示例一维数据点
data = Createtime
# 设定距离阈值δ
delta = 3600
# 初始化一个空列表,用于存储聚类结果
clusters = []
current_cluster = []
# 遍历数据点
for i in range(len(data)):
# 如果current_cluster为空,或者当前点与上一个聚类点的距离小于等于delta
if current_cluster == [] or (len(current_cluster) > 0 and abs(data[i] - current_cluster[-1] <= delta)):
# 添加到当前聚类
current_cluster.append(data[i])
else:
# 否则,保存当前聚类并开始新的聚类
clusters.append(current_cluster)
current_cluster = [data[i]]
# 保存最后一个聚类(如果有的话)
if current_cluster:
clusters.append(current_cluster)
注意此处若你想把聚类阈值设为两个小时(两个小时没人说话就分新一类)可以把delta设置为7200
Createtime是time的连续版本(两个时间相差的秒数就等于两个Createtime的差值),可以通过字典实现Createtime与Strtime之间的一一对应
timemap = []
for i in clusters:
if len(i)>=2:
timemap.append(i)
此处是抛弃那些只有一个人说了话的话题,把话题对应createtime记录在timemap里
二、实现每个人的话题参与向量
描述很多个人在很多个话题中的发言情况时,如果一个人对某个话题说了话则标记为1,没说话则标记为0
,如此可得n个人的话题参与向量(m个话题的话为m*1的向量)
data = [[0 for i in range(len(timemap))] for z in range(len(nickname))]
for k,i in enumerate(timemap):
namelst = [dict_name[q] for q in i]
for p,z in enumerate(nickname):
if z in namelst:
data[p][k]=1
三、描述两个人聊天的相关性(方法一)
此处提供了两个个分析方法,data1,2都是n×n的矩阵,data1的第i行第j列意味着n个人里面第i个人的话题参与向量预测第j个人的话题参与向量得到的auc值
data2的第i行第j列意味着n个人里面第第i个人参与了的话题,第j个人参与了多少(百分比占比多少)
data1=[[0 for i in range(len(nickname))] for j in range(len(nickname))]
data2=[[0 for i in range(len(nickname))] for j in range(len(nickname))]
for i,j in enumerate(nickname):
for p,q in enumerate(nickname):
data1[i][p] = roc_auc_score(data[i], data[p])
count1 = 0
count2 = 0
for k in range(len(timemap)):
if data[i][k]==1:
count2+=1
if data[i][k]==1 and data[p][k]==1:
count1+=1
data3[i][p] = count1/count2
四、描述两个人聊天的相关性(方法二)
也可以用接话程度去描述一个人是不是喜欢另一个人,我把每个话题,谁接这个人话接最多,那统计出来的矩阵人A和人B对应的值就会+1,最后总体来看谁接这个人话最多~
data3 = [[0 for i in range(len(nickname))] for z in range(len(nickname))]
for i in timemap:
namelst = [dict_name[p] for p in i]
for k in range(len(nickname)):
q_lst = [0 for i in range(len(nickname))]
for z,j in enumerate(namelst):
if z == len(i)-1:
break
if j == dic_intname[k]:
q_lst[dic_nameint[namelst[z+1]]]+=1
# print(q_lst)
q_lst[k]=0
for i1,i2 in enumerate(q_lst):
if i2 == max(q_lst) and max(q_lst) != 0:
data3[k][i1]+=1
五、绘制热力图
(想画data几的就第一行输入data几)
for i in range(len(nickname)):
data1[i][i]=0
map = pd.DataFrame(data1)
plt.figure(figsize=(10, 10))
plt.rcParams['font.sans-serif'] = ['SimHei']
realname = [dict_realname[i] for i in nickname]
sns.heatmap(map, annot=True, cmap="YlGnBu")
plt.title('丘比特的箭靶子')
plt.xticks(ticks=range(len(nickname)), labels=nickname, rotation=90) # 旋转90度以便竖着显示
plt.yticks(ticks=range(len(nickname)), labels=nickname, rotation=360)
plt.xlabel('群友')
plt.ylabel('群友')
plt.show()
六、看图
然后就好啦,展示一下群主画的热力图吧~
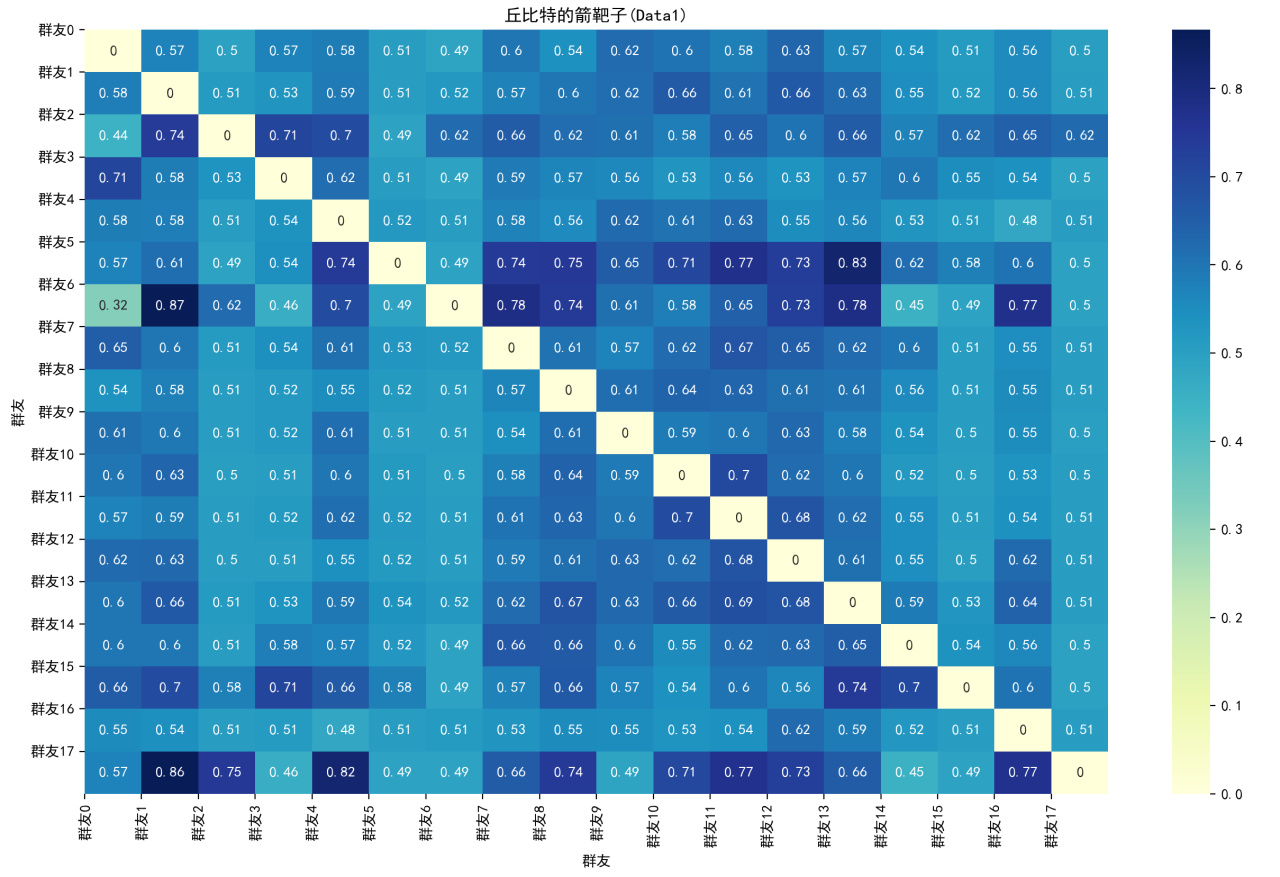
Data1的,这里的值为0.5意味着平常,相对而言大意味着显著
此处i(行数),j(列数)点代表着群友i的发言频率可以推测出群友j的发言频率的概率,如果高,意味着j的发言有可能是受到i影响,如果某个男人的发言只会被很多男生和一个女生影响,那意味着上面不必多说吧~
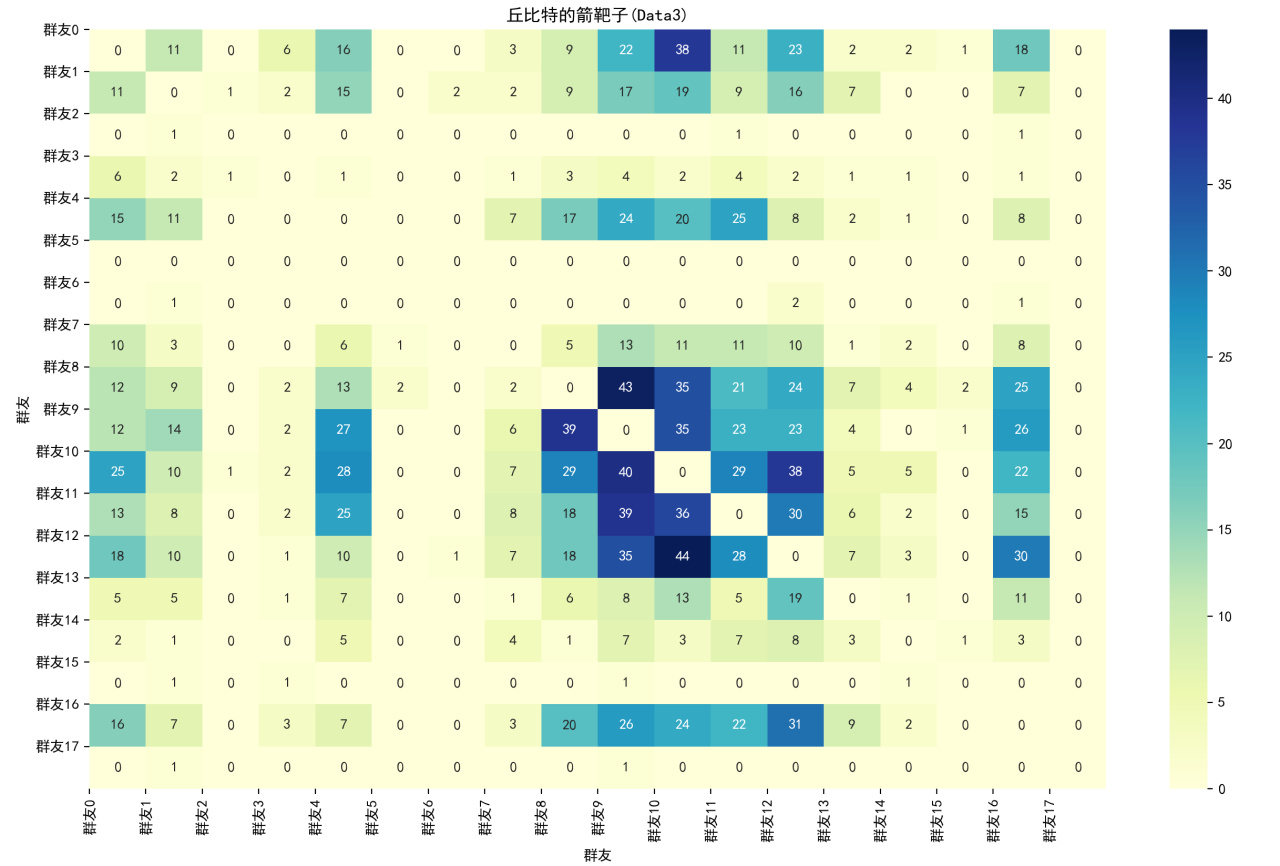
Data3的,数值越大意味着横轴作为纵轴话题接话最多者的次数
此处,楼主刚开始说到的男女生分别为群友4和7,实践发现他们是接对方话接的话题最多的异性,而且是断档领先,由此得知~~
此外,也可以由data2看第二个人因第一个人出现而出现的频率是多少~图就先不放了哈~~
七、尾声
大概就是这样~~其实这篇文章的还未找到明确的文章依据(微信群聊天怎么样才是一个人喜欢另一个人哈)本文的依据是一个人对另一个人有意思,那么两个人共同参与话题的可能性就会更大以及第二个人接第一个人话的可能性会更大。如果有优秀的心理学社会学盒友能帮忙把这一块依据补上那真是万分感激~~~

如果有其他八卦头子有其他八卦方法也欢迎在评论区一起讨论呀
文中哪里有问题的也欢迎随时评论区批判我
最后还是声明一下,如果群里有朋友介意这种分析 那最好就不要做啦
更多游戏资讯请关注:电玩帮游戏资讯专区
电玩帮图文攻略 www.vgover.com


















