最烧脑解密-三神谜题

放国庆长假放得脑袋整天昏昏沉沉的，来玩点烧脑小游戏吧，最近复习了一下离散数学，来看看逻辑推理谜题-三神谜题的问题描述。

1996年，数学逻辑学家George Boolos（下图）发表了一篇论文，描述了“有史以来最难的逻辑难题”，他将其归因于逻辑学家Raymond Smullyan，我们首先来看一下问题的翻译版本：

问题重述

“A、B、C三个神，按顺序被称为True、False和Random。True总是说真话，False总是说假话，Random说真话还是假话完全是随机的。你的任务是通过问三个问题来确定A、B和C的身份；每个问题都必须问一个神。神懂英语（你理解成懂中文也行），但会用他们自己的语言回答所有问题，其中“是”和“否”的单词按某种顺序是“da”和“ja”。你不知道哪个词意味着哪个。” 你的目标是确定谁是真神(True)、谁是伪神（False，或者可以叫做假神）、谁是随机神（Random）。

论文截图来自MIT technology review

对于该谜题，George Boolos给出了一些约束：

• 允许一位神被问到了不止一个问题（有些神可能根本没有被问到任何问题）。

• 第二个和第三个问题的内容和指向哪位神可以依赖于之前问题的答案（即可以根据第一个问题的答案再决定向哪位神问第二个问题、第二个问题的内容是什么）。

• 可以认为随机神脑子里有一枚（理想的）硬币，随机神在回答问题之前会先在脑中掷币，然后根据掷币结果决定自己是给出与真实情况相同的回答、还是给出与真实情况相反的回答。（也就是说即使三个问题都问随机神，他可能也不会一直说真话或者一直说假话。）当被问及是非问题时，随机神将回答da或者ja。

在观看下面的分析之前，大家可以先想一下该如何提问？

简化问题分析，如果没有随机神？

看完整个问题我们可以稍微梳理一下，如果没有随机神，那么问题可以怎么分析呢？考虑一个很常见的逻辑题，如果你走到一条岔路上，前面遇到两个人，一个人永远说真话，一个人永远说假话，你并不知道谁说真话谁说假话，只许问其中一个人一句话，该如何发问？

这里可以运用一个不太常见的问题，可以叫做嵌入式问题引理。我们随便问一个人：你知道另一个人会把哪条路指为正确的路吗？对方回答后，你选择答案的另一条路即可。分析如下：

假设A身后的路是真的说真话，你问他:你觉得我问B：你身后的路是不是真的，它会怎么回答我？

这时候A如果说：B会回答真的

注意A说的真话，那么b身后的路就会是假的。

同理：假设A说的假话是假的路，问A:你觉得我问B：你身后的路是不是真的，它会怎么回答我

A说：B会回答假的。

那么B路就是真的。所以不管你怎么问，问谁，都会得到相反的答案，这时候你只要走相反的就行了

回到三神问题本身，作者Boolos的解法

其实Boolos 在论文中发表的解决方案并没有使用嵌入问题的方法，他提出的问题是：“当且仅当 B 是随机神时，当且仅当你是真神时，da 是否意味着是？”，就是说Boolos 使用了两个条件假设，侧重于通过复杂的问题找到 True 或 False。这个复杂问题也很有意思，相当于你说“当且仅当罗马在俄罗斯，月亮是由山东大学制成的”，那么你就做出了正确的陈述，因为它的两部分都是错误的。“当且仅当罗马在意大利时，月亮没有空气”这句话也是正确的，因为它的两个部分都是正确的。

逻辑推理过程大概是这样的(我自己推的，可能有错误，欢迎指正)：

一、分析第一阶段提问

首先向神 A 提问“当且仅当 B 是随机的，‘da’是否意味着你是真的？”，这个问题的巧妙之处在于无论 A 的回答是什么，都能得到有用的信息：

1. 如果 A 是真或假，得到答案“da”： 可以推断出 B 是随机神。进而知道 C 要么是真，要么是假。

2. 如果 A 是真或假，得到答案“ja”： 可知 B 不是随机神。 所以 B 要么是真，要么是 False。

3. 如果 A 是随机，得到答案“da”： 能推出 C 不是随机神（同时 B 也不是随机神，但此时 B 的情况无关紧要）。 -因此 C 要么是真，要么是假。

4. 如果 A 是随机，得到答案“ja”： B 不是随机神（C 也不是随机神，同样此时 C 的情况无关紧要）。 所以 B 要么是真，要么是假。

总之，“da”的回答确保 C 不是随机神，“ja”的回答对 B 有同样的确定作用，即能确定 B 不是随机神。

二、分析第二阶段提问

接着，通过一个已知部分准确的问题“当且仅当罗马在意大利时，da 的意思是吗？”来确定面对这个问题时 True 和 False 的回答规律，即 True 会说“da”，False 会说“ja”。

三、分析第三阶段提问

最后向同一个神提问“当且仅当 A 是随机神，da 的意思是是吗？”，通过这个问题的回答以及前面的排除过程，就可以确切地知道三个神分别是谁。 整个推理过程利用了逻辑等价和排除法，通过巧妙的提问设计逐步缩小可能性范围，最终确定三个神的身份。

怎么用嵌套问题快速求解？

能不能用之前提到的嵌套的方式来绕开复杂的条件假设呢？答案是可以，这个解法也是目前中文互联网中最常见的解法，借用知乎文章深入浅出带你看懂最烧脑逻辑题——布洛斯谜题解题思路来简单介绍一下。

可以模仿之前的“嵌套问题”，让三位神站/坐成一排，左到右为A——B——C

提问策略为：

1）先向A提问，A地回答为ja的话接下来对B提问，否则向C提问。

2）第3个提问和第2个都是同一位神。

3）根据提问的得到的回答可以达到8种组合，按照下表可以唯一地确定ABC三位神地身份。

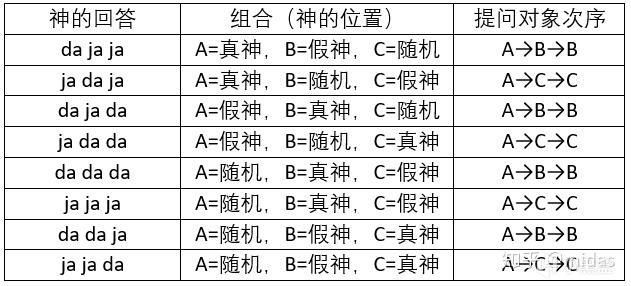
提问则是：
1）假神是在随机神左边的答案是da吗？
2）真神在假神左边或者随机在假神右边的答案是da吗？
3）da=对吗？

总结一下

三神谜题的难点在于随机神的存在让我们很难构筑简单的问题，迷题的解法也很多，但无论是哪一种，归根到底相当于把复杂的逻辑层层剥开，一步一步简化我们的问题设计，最关键的是要抓住每个回答所提供的信息。这一点在密码学中也非常重要，即时伪神给出了错误的答案，但是错误的答案也同样提供了信息，可以利用这种信息来分析问题。